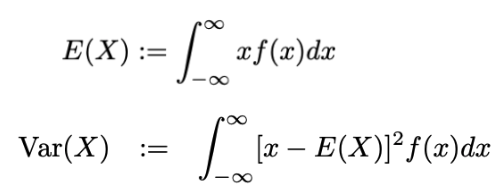Data generated from Scipy truncnorm.rvs does not match specified standard deviation-CodePudding

I am trying to generate data which follow specified truncated normal distribution. Based on answers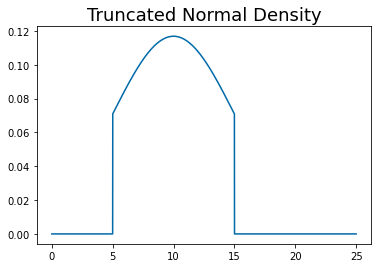

showcases the truncated normal density alluding to the fact that the narrower the interval [lower, upper] are chosen, the smaller the standard deviation will be (even approaching 0 asymptotically when lower and upper get infinitesimally close).

Let's make this rigorous to really be sure. Given the age-old equations for the expected value and variance of our (truncated normal random variable X) we have

Then, defining the helper functions

def xfx(x, lower=lower, upper=upper, mu=mu, sigma=sigma):
    '''helper function returning x*f(x) for the truncated normal density f'''
    return x*scipy.stats.truncnorm.pdf(x, (lower-mu)/sigma, (upper-mu)/sigma, loc=mu, scale=sigma)

def x_EX_fx(x, lower=lower, upper=upper, mu=mu, sigma=sigma):
    '''helper function returning (x - E[X])**2 * f(x) for the truncated normal density f'''
    EX = quad(func=xfx,a=lower,b=upper)[0]
    return ((x - EX)**2) * scipy.stats.truncnorm.pdf(x, (lower-mu)/sigma, (upper-mu)/sigma, loc=mu, scale=sigma)

allows us to compute the values exact

# E[X], expected value of X
quad(func=xfx,a=lower,b=upper)[0]
> 10.0

# (Var(X))^(1/2), standard deviation of X
np.sqrt(quad(func=x_EX_fx,a=lower,b=upper)[0])
> 2.697

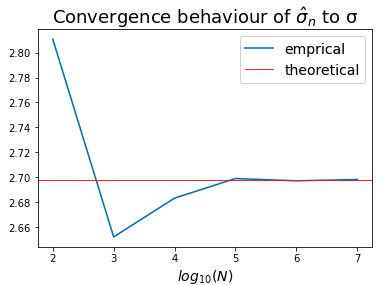
This looks eerily similar to your observed value 2.673. Let's see if the difference is merely based on the finite sample size by running a simulation study to observe if the empirical standard deviation approaches the theoretical one.

# simulation study
np.random.seed(7447)
stdList = [scipy.stats.truncnorm.rvs((lower-mu)/sigma, (upper-mu)/sigma, loc=mu, scale=sigma, size=round(10**N)).std() for N in range(2,8)]

# plot 
plt.title("Convergence behaviour of $\hat{σ}_{n}$ to σ", fontsize=18)
plt.plot(range(2,8), stdList)
plt.axhline(2.697800468774485, color='red', lw=0.85)
plt.legend({'emprical' : 'blue', 'theoretical' : 'red'}, fontsize=14)
plt.xlabel("$log_{10}(N)$", fontsize=14)
plt.show()

yielding

This confirms that your output is sound,

CodePudding user response：

This is generating a clipped normal distribution between [5,15]. This is /- 1 s.d, so the s.d. measured across this sample will not be equal to the input.

If you clip the range of outputs, you necessarily reduce the s.d. observed.

As lower/upper -> /-infinity, the sample std -> 5. As lower/upper -> 10, the sample std -> 0.