Should features that correlate be deleted from ML models?-CodePudding

I've seen that it's common practice to delete input features that demonstrate co-linearity (and leave only one of them).

However, I've just completed a course on how a linear regression model will give different weights to different features, and I've thought that maybe the model will do better than us giving a low weight to less necessary features instead of completely deleting them.

To try to solve this doubt myself, I've created a small dataset resembling a x_squared function and applied two linear regression models using Python:

A model that keeps only the x_squared feature
A model that keeps both the x and x_squared features

The results suggest that we shouldn't delete features, and let the model decide the best weights instead. However, I would like to ask the community if the rationale of my exercise is right, and whether you've found this doubt in other places.

Here's my code to generate the dataset:

# Import necessary libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# Generate the data
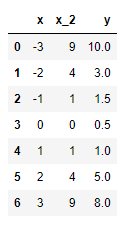
all_Y = [10, 3, 1.5, 0.5, 1, 5, 8]
all_X = range(-3, 4)
all_X_2 = np.square(all_X)

# Store the data into a dictionary
data_dic = {"x": all_X, "x_2": all_X_2, "y": all_Y}

# Generate a dataframe
df = pd.DataFrame(data=data_dic)

# Display the dataframe
display(df)

which produces this:

and this is the code to generate the ML models:

# Create the lists to iterate over
ids = [1, 2]
features = [["x_2"], ["x", "x_2"]]
titles = ["$x^{2}$", "$x$ and $x^{2}$"]
colors = ["blue", "green"]

# Initiate figure
fig = plt.figure(figsize=(15,5))

# Iterate over the necessary lists to plot results
for i, model, title, color in zip(ids, features, titles, colors):
    
    # Initiate model, fit and make predictions
    lr = LinearRegression()
    lr.fit(df[model], df["y"])
    predicted = lr.predict(df[model])
    
    # Calculate mean squared error of the model
    mse = mean_squared_error(all_Y, predicted)
    
    # Create a subplot for each model
    plt.subplot(1, 2, i)
    plt.plot(df["x"], predicted, c=color, label="f("   title   ")")
    plt.scatter(df["x"], df["y"], c="red", label="y")
    plt.title("Linear regression using "   title   " --- MSE: "   str(round(mse, 3)))
    plt.legend()

# Display results
plt.show()

which generate this:

What do you think about this issue? This difference in the Mean Squared Error can be of high importance on certain contexts.

CodePudding user response：

So x2 and y are highly correlated and you are trying to predict y with x2? A high correlation between predictor variable and response variable is usually a good thing - and since x and y are practically uncorrelated you are likely to "dilute" your model and with that get worse model performance.

(Multi-)Colinearity between the predicor variables themselves would be more problematic.

CodePudding user response：

Because x and x^2 are not linear anymore, that is why deleting one of them is not helping the model. The general notion for regression is to delete those features which are highly co-linear (which is also highly correlated)