Verify that a number can be decomposed into powers of 2-CodePudding

Is it possible to verify that a number can be decomposed into a sum of powers of 2 where the exponents are sequential?

Is there an algorithm to check this?

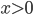Example: where and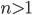

CodePudding user response：

This can be done in an elegant way using bitwise operations to check whether the binary representation of the number is a single block of consecutive 1 bits, followed by perhaps some 0s.

The expression x & (x - 1) replaces the lowest 1 in the binary representation of x with a 0. If we call that number y, then y | (y >> 1) sets each bit to be a 1 if it had a 1 to its immediate left. If the original number x was a single block of consecutive 1 bits, then the result is the same as the number x that we started with, because the 1 which was removed will be replaced by the shift. On the other hand, if x is not a single block of consecutive 1 bits, then the shift will add at least one other 1 bit that wasn't there in the original x, and they won't be equal.

That works if x has more than one 1 bit, so the shift can put back the one that was removed. If x has only a single 1 bit, then removing it will result in y being zero. So we can check for that, too.

In Python:

def is_sum_of_consecutive_powers_of_two(x):
    y = x & (x - 1)
    z = y | (y >> 1)
    return x == z or y == 0

Note that this returns True when x is zero, and that's the correct result if "a sum of consecutive powers of two" is allowed to be the empty sum. Otherwise, you will have to write a special case to reject zero.

CodePudding user response：

The binary representation would have a single, consecutive group of 1 bits.

To check this, you could first identify the value of the least significant bit, add that bit to the original value, and then check whether the result is a power of 2.

This leads to the following formula for a given x:

x & (x   (x & -x)) == 0

This expression is also true when x is zero. If that case needs to be rejected as a solution, you need an extra condition for that.

In Python:

def f(x):
    return x > 0 and x & (x   (x & -x)) == 0

CodePudding user response：

A number can be represented as the sum of powers of 2 with sequential exponents iff its binary representation has all 1s adjacent.

E.g. the set of numbers that can be represented as 2^n 2^n-1, n >= 1, is exactly those with two adjacent ones in the binary representation.

CodePudding user response：

just like this:

bool check(int x) {/*the number you want to check*/
    int flag = 0;
    while (x >>= 1) {
        if (x & 1) {
            if (!flag) flag = 1;
            if (flag == 2) return false;
        }
        if (flag == 1) flag = 2;
    }
    return true;
}

O(log n).