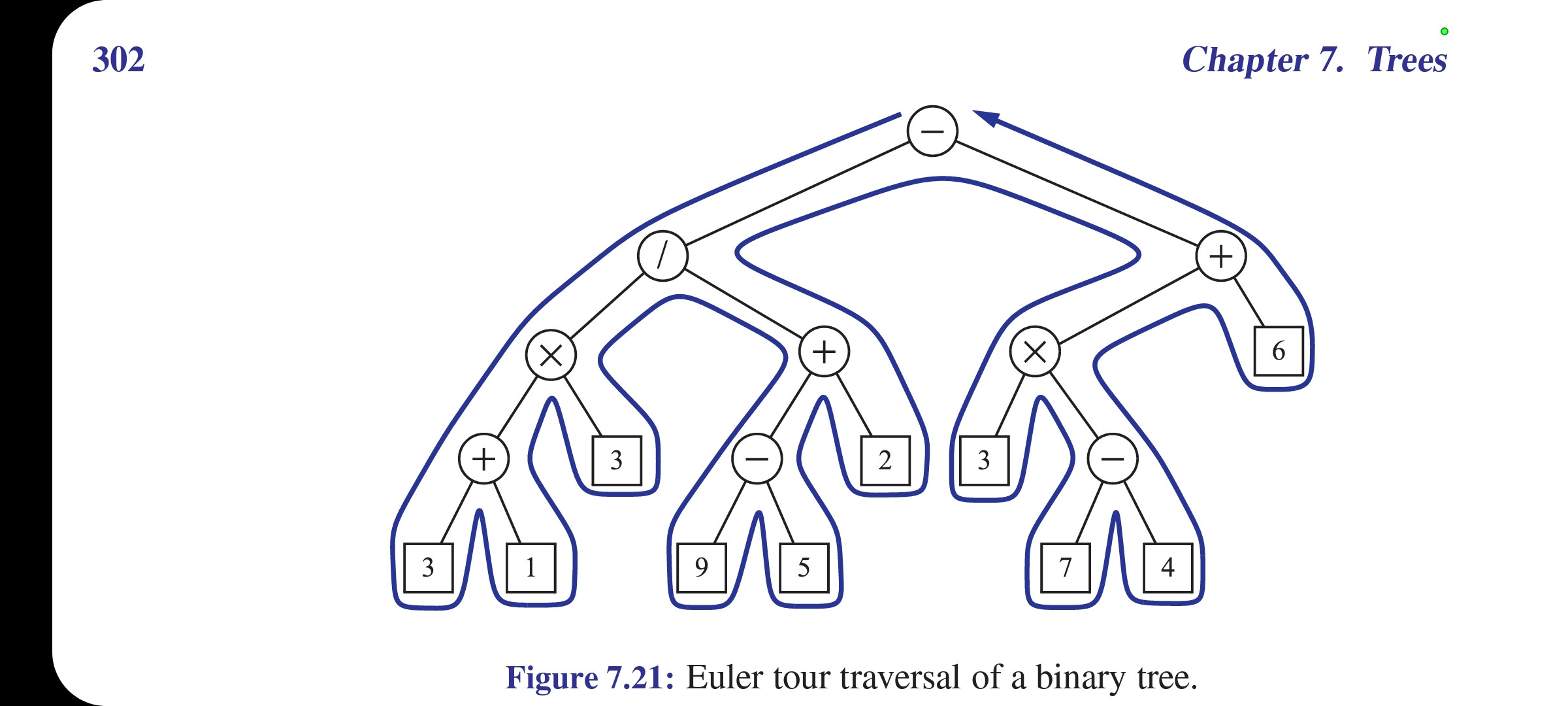
Below is the euler tree.

According to author:

To determine the number of descendants of a node p, we COMPUTE THE DIFFERENCE between the values of the counter when p is visited on the left and when it is visited on the right, and add 1. This simple rule gives us the number of descendants of p, because each node in the subtree rooted at p is counted between p’s visit on the left and p’s visit on the right. Therefore, we have an O(n)-time method for computing the number of descendants of each node in T.

I can't figure out how the above statement would work on counting number of descendants for a node p.
Any help with example how it works would be great.

CodePudding user response：

Imagine doing an Euler tour of the tree. Focus on some node p in the tree. Write down the value of the counter when p is visited on the left; call it c_before. Then, write down the value of the counter when p is visited on the right; call it c_after. The author is proposing that you look at the value c_after - c_before 1.

Why does this work? Once the Euler tour has descended down to the left of the node p, the counter will be incremented once for every node it finds. Until the Euler tour comes back up to p, all the nodes that are found will be descendants of p (they're beneath p). Therefore, at the point where the Euler tour comes back up to p, the counter will have been incremented once for each node that is a proper descendant of p (here, "proper descendant" means "a descendant of p that isn't p itself), and so c_after - c_before counts the number of proper descendants of p.

We then just need to add 1 to account for p itself.

CodePudding user response：

Here is a function in Python that performs an Euler tour and uses a counter that counts the nodes as they are traversed.

The counter is printed before a node's left tree is visited, and after its right tree is visited. This illustrates how that counter difference corresponds to the number of visited nodes.

The tree used as example is this one:

          B
         / \
        A   D
           / \
          C   E

from collections import namedtuple

# simple Node "class"
Node = namedtuple("Node", "value, left, right", defaults=(None, None))

def euler_traversal(root: Node): 
    # A single variable accessed by the recursive calls of below function
    counter = 0  
    
    # Helper function which is called recursively
    def euler_traversal_rec(node: Node, indent):
        nonlocal counter

        if node is None:  # Base case
            return 0
        incoming = counter  # Remember what counter is on first visit
        print(f"{indent}Passing node {node.value} at left side, and counter is {counter}")
        euler_traversal_rec(node.left, indent   "  ")
        euler_traversal_rec(node.right, indent   "  ")
        print(f"{indent}Passing node {node.value} at right side, and counter is {counter}")
        size = counter - incoming
        print(f"{indent}...so node {node.value} has {counter} - {incoming} = {size} descendants")
        counter  = 1  # Add 1 for the current node

    # Start the traversal
    euler_traversal_rec(root, "")

# Demo tree
root = Node("B", 
    Node("A"),
    Node("D",
        Node("C"),
        Node("E")
    )
)
euler_traversal(root)

This program generates this output:

Passing node B at left side, and counter is 0
  Passing node A at left side, and counter is 0
  Passing node A at right side, and counter is 0
  ...so node A has 0 - 0 = 0 descendants
  Passing node D at left side, and counter is 1
    Passing node C at left side, and counter is 1
    Passing node C at right side, and counter is 1
    ...so node C has 1 - 1 = 0 descendants
    Passing node E at left side, and counter is 2
    Passing node E at right side, and counter is 2
    ...so node E has 2 - 2 = 0 descendants
  Passing node D at right side, and counter is 3
  ...so node D has 3 - 1 = 2 descendants
Passing node B at right side, and counter is 4
...so node B has 4 - 0 = 4 descendants