I know how to get periment and area when an input is 3 coordinates of triangle. But if input is periment and area, How can i get 3 coordinates? For example,

input(periment, area) : 12, 6

output(a, b, c) : (0, 0), (3, 0), (3, 4)

something like that. Mathematically how can i get the coordinates of the triangle? I need an explanation please.

CodePudding user response：

Let's say point a and b's x are opposites.

d = 2, d > 0

A = (-d, 0), b = (d, 0), or any opposites

Aka: (-2, 0) (2, 0)

A = bh/2

We already have b, which is the absolute value of either a or b, * 2. We can get h, which is c_y, which is 0 on the x axis. Think about it, the middle of a and b will always be (0, 0) as long as x's are opposites. We already have A, which you provided. So, we must solve for h.

A = bh/2

2A = bh

2A/b = h

2A/(2d) = h

A/d = h

Finally

d = p / 6

a = (-d, 0)

b = (d, 0)

c = (0, A/d)

All in all

The perimeter is not perfectly acurate, but d = p / 6 is a good estimate for your triangle. You would have to redo this equation over and over again to get the perimeter closer. Using an area of 6 and perimeter of 12, would create a triangle with exactly 6 area, and in between 11 and 12 perimeter.

CodePudding user response：

You can calculate the coordinates of one of the possible triangles following these steps:

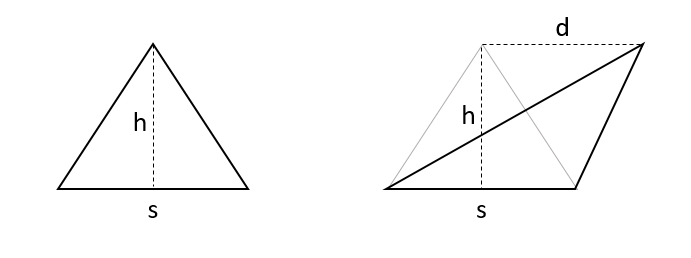
1. Take the area and calculate the edge length s and the height h of the corresponding equilateral triangle. Perimeter of this triangle is 3s and this obviously is the smallest perimeter for the given area you can achieve.
2. Take one edge of the equilateral triangle as baseline of your target triangle and keep its length s.
3. Take the opposite point of the baseline and shift it parallel to the baseline by some shifting distance d, keeping the height h constant. The area of the triangle will be kept constant and the perimeter will steadily increase.
4. This way iteratively approximate the value d until the triangle has the requested perimeter.

Or the whole thing vice versa keeping the perimeter constant and lowering the area.

The formulas for area, height and perimeter are well documented.