Generate Permutation With Minimum Guaranteed Distance from Elements in Source-CodePudding

Given a sequence a with n unique elements, I want to create a sequence b which is a randomly selected permutation of a such that there is at least a specified minimum distance d between duplicate elements of the sequence which is b appended to a.

For example, if a = [1,2,3] and d = 2, of the following permutations:

a         b
[1, 2, 3] (1, 2, 3) mindist = 3
[1, 2, 3] (1, 3, 2) mindist = 2
[1, 2, 3] (2, 1, 3) mindist = 2
[1, 2, 3] (2, 3, 1) mindist = 2
[1, 2, 3] (3, 1, 2) mindist = 1
[1, 2, 3] (3, 2, 1) mindist = 1

b could only take one of the first four values since the minimum distance for the last two is 1 < d.

I wrote the following implementation:

import random
n = 10
alist = list(range(n))

blist = alist[:]

d = n//2

avail_indices = list(range(n))
for a_ind, a_val in enumerate(reversed(alist)):
  min_ind = max(d - a_ind - 1, 0)
  new_ind = random.choice(avail_indices[min_ind:])
  avail_indices.remove(new_ind)
  blist[new_ind] = a_val
print(alist, blist)

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9] [1, 3, 2, 8, 5, 6, 4, 0, 9, 7]

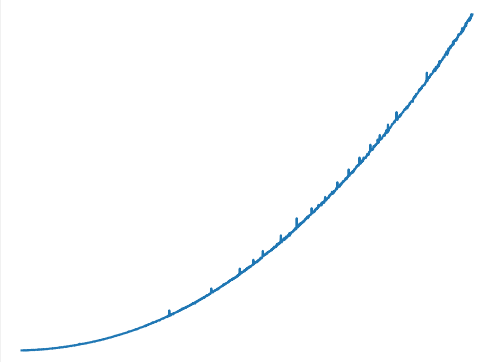
but I think this is n^2 time complexity (not completely sure). Here's a plot of the time required as n increases for d = n//2:

Is it possible to do better than this?

CodePudding user response：

Yes, your implementation is O(n^2).

You can adapt the Fisher-Yates shuffle to this purpose. What you do is work from the start of an array to the end, placing the final value into place out of the remaining.

The trick is that while in a full shuffle you can place any element at the start, you can only place from an index that respects the distance condition.

Here is an implementation.

import random

def distance_permutation (orig, d):
    answer = orig.copy()
    for i in range(len(orig)):
        choice = random.randrange(i, min(len(orig), len(orig)   i - d))
        if i < choice:
            (answer[i], answer[choice]) = (answer[choice], answer[i])
    return answer


n = 10
x = list(range(n))
print(x, distance_permutation(x, n//2))