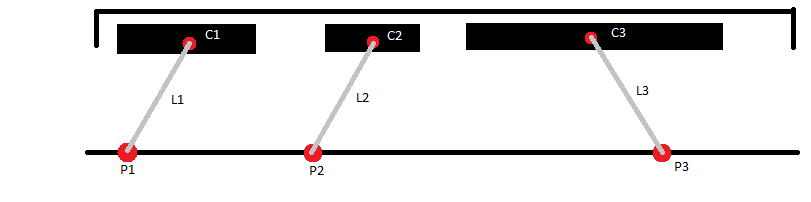
I am trying to find an optimal way to place a set of ranges in a larger range. I like to think of it as flat boxes that can move left or right. Some things to consider:

• There are N boxes, each of them with a center point Ci.
• There are N attractor points (one per box), we can call them Pi. Each box is attracted to one attractor point with a force proportional to the distance.
• The order of the boxes is fixed. The order of the attractor points and of the boxes is the same. So C1 is attracted to P1, C2 to P2, etc.
• The boxes cannot overlap.

I made a diagram that may make it easier to understand:

The question is, what algorithm can I use to move the boxes around so that each Ci is the closest possible to its respective Pi. In other words, how do I find the locations for the Ci points that minimizes the distance (Li) between all Ci-Pi pairs?

I'd also be helpful if you can point me in to some material to read or something, I'm not very familiar with this type of problems... My guess is that some sort of force-directed algorithm would work but I'm not sure how to implement those.

CodePudding user response：

Edit: this is a crude solution to minimize the sum of all Li, which is no longer the question.

Let's name the boxes B, so Bi has center Ci. Let n be the number of boxes and points. Assuming all the boxes can fit into the larger range, here is how I would do it:

Let Q(a, b) be the average of Pi from i=a to i=b.
Place all the boxes next to each other (in order) to form a superbox, so that the center of this superbox is at Q(1, n). If it goes over one end of the larger range, move it so that it sits at the limit.

Then, for each Bi, move it as close to Pi as possible without moving other boxes (and while still being inside the larger range). Repeat until you can't move any more box.

Now, the only way to minimize the sum of all Li is as follows.
Let G be a group of boxes that touch. Let F(G) be the predicate: if the center boxes of a series are Bi and Bj (if there are an odd number of boxes in the series, i=j), then Ci != Pi and Cj != Pj.
Find a G such that F(G) is true, and move the corresponding boxes so that F(G) becomes false. If the group of boxes hit another box while moving, add that box to the group and repeat. Of course, don't move any box outside the larger range.

Once there is no G for which F(G) is true or for which you would need to move outside the larger range, you have your solution (one of potentially an infinite number).

CodePudding user response：

Since "each box is attracted to one attractor point with a force proportional to the distance", you are describing a system where the boxes are attached to the attractor points by springs (see Hooke's law), and you want to determine the state of the system at rest (the state of minimum potential energy).

Because the forces are proportional to the distances, what you want is to minimize the sum of the distances squared, or the sum of Li^2 from i=0 to i=n. Here is an algorithm to do that.

The idea is to group boxes that need to touch by the end and figure out their position as a group based on their corresponding attractor points.

The first step is not to find these groups, because we can actually start with one big group and cut it later if necessary. For simplicity, let's treat all Li as signed distances. So Li = Ci-Pi. Let's also name the sizes of the boxes, though it will be easier to handle half-sizes. So let Si be half the size of the i-th box. Finally, let's write the sum of Xi from i=a to i=b like sum[a,b](Xi).

Here is how to compute the position of a group of boxes, assuming each one touches the next. Li is a function of the position of the group: if x is that position, Li(x) = Ci(x) - Pi (where Ci(x) is just x plus some constant). x can be point of the group of box, for example the left edge of the first box.
We also know that sum[a,b](Li(x)^2) must be minimal. This means the derivative of that sum must be zero: sum[a,b](2*Li(x)) = 0. So:

sum[a,b](2*Li) = 0
sum[a,b](Li) = 0
sum[a,b](Ci - Pi) = 0
sum[a,b](Ci) = sum[a,b](Pi)

Computing sum[a,b](Pi) is trivial, and sum[a,b](Ci) can be expressed in terms of Ca (center of the first box), since C[i 1] = Ci Si S[i 1].

Now that you can compute the position of a group of boxes, do it first with a group made of all boxes, and then remove boxes from that group as follows.
Starting from the left, consider all boxes with Li > 0 and compute Q = sum(Li) for all corresponding i. Similarly, starting from the right, consider all boxes with Li < 0 and compute R = -sum(Li) for all corresponding i (note that negative sign, because we want the absolute value). Now, if Q > R, remove the boxes on the left and make a new group with them, otherwise remove the boxes on the right and make a new group with them.
You cannot make these two new groups at the same time, because removing boxes from one end can change the position of the original group, where boxes you would have removed from the other end should not be removed.

If you made a new group, repeat: compute the position of each separate group of boxes (they will never overlap at this point), and remove boxes if necessary. Otherwise, you have your solution.

CodePudding user response：

It seems the objective is a quadratic function and all the constraints are linear. So I think you can solve it by standard quadratic programming solvers. If we write S_i be the half-size of i-th box, and the Pi's are given, then:

Minimize y 
with respect to C_1, C_2, ...C_n

subject to

y = sum_i (P_i - C_i)^2
C_i   S_i   S_{i 1} <= C_{i 1}   for each i = 1, ... n-1