How Many Ways are There to Order the Letters of a Word using google sheets-CodePudding

Determine the number of distinct ways to arrange the letters for each word in the range A1:A18.

For example the word arrangement

Formula:

                   n!
nPr =      -------------------
           (n1! n2! . . . nr!)

In the (nPr) permutation equation, place the values retrieved from the term arrangement.

                   11!
nPr =    ----------------------- 
         (2! 2! 2! 1! 2! 1! 1! )

    1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11
=  ---------------------------------------------
   {(1 x 2) (1 x 2) (1 x 2) (1) (1 x 2) (1) (1)}

nPr of word arrangement = 2494800

As a result, the letters in the word arrangement may be arranged in 2494800 distinct ways.

CodePudding user response：

Factorial can be easily found with FACT. Unique letter count is a bit complicated, but once we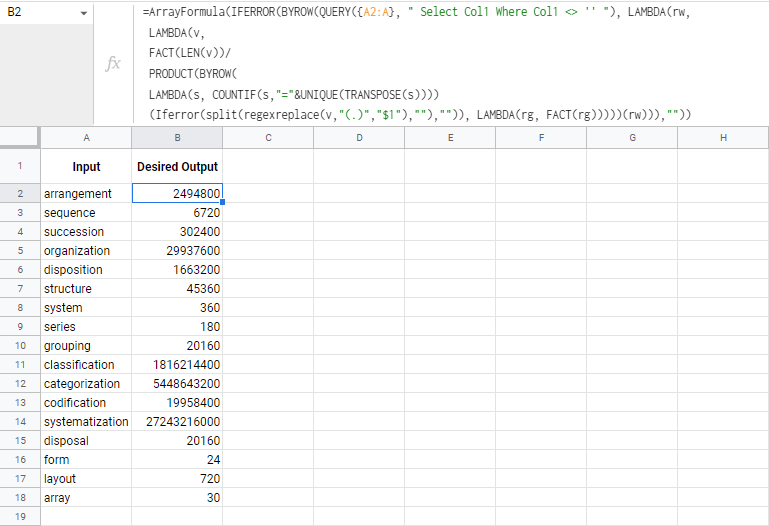

Simplified like this:

factorial of (Length of the (Range)) / Product of factorial of each sum of unique letter count