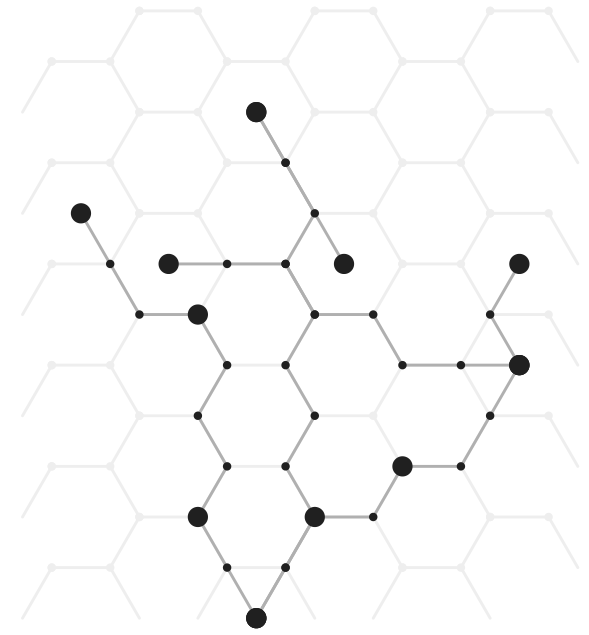
Background

Looking to trace a path between two points on a hexagonal grid while following the nearest edge.

Problem

Determining the algorithm to constrain the all iterations after the first one to the edge.

Code

Given:

vac -- The X coordinate of the starting vertex.
var -- The Y coordinate of the starting vertex.
vbc -- The X coordinate of the ending vertex.
vbr -- The Y coordinate of the ending vertex.
offset_ac -- The X grid offset for the starting central point.
offset_ar -- The Y grid offset for the starting central point.

We can compute:

theta -- The angle of the line, in degrees, between the starting and ending points.
vangle -- The nearest vertex to the line (based on angle).
vc -- The X coordinate of the first vertex, offset from the center.
vr -- Ditto for the Y coordinate.

% Compute the direction towards the first segment (to vertex of an edge).
theta := degrees( atantwo( vac, var, vbc, vbr ) );
vangle := round( theta / 60 ) * 60 * pi / 180;

% Calculate the position of the first vertex, offset from the center.
vc := offset_ac   cos( vangle );
vr := offset_ar   sin( vangle );

% Draw a line from the starting point to the ending point.
draw (offset_ac, offset_ar) -- (vc, vr)
  withcolor colour_node;

% Draw a circle at the ending coordinate.
draw (vc, vr)
  withcolor colour_node
  withpen pencircle
  scaled vertex_sm;

Output

The current output resembles:

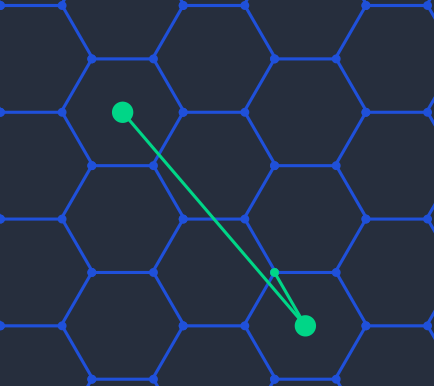
The desired output resembles:

Question

What algorithm can walk the graph between the starting and ending points while the path is constrained to the edges?

Finding the first vertex was simple enough. Conceptually, the given code seems like it could be iterated over with the correct "shifting" of the starting point's offset to the vertex. However, after such a "shift" would the new angles be incorrect by something like a half-width and half-height? And even then, how would you keep the next iteration constrained as depicted in the second diagram?

CodePudding user response：

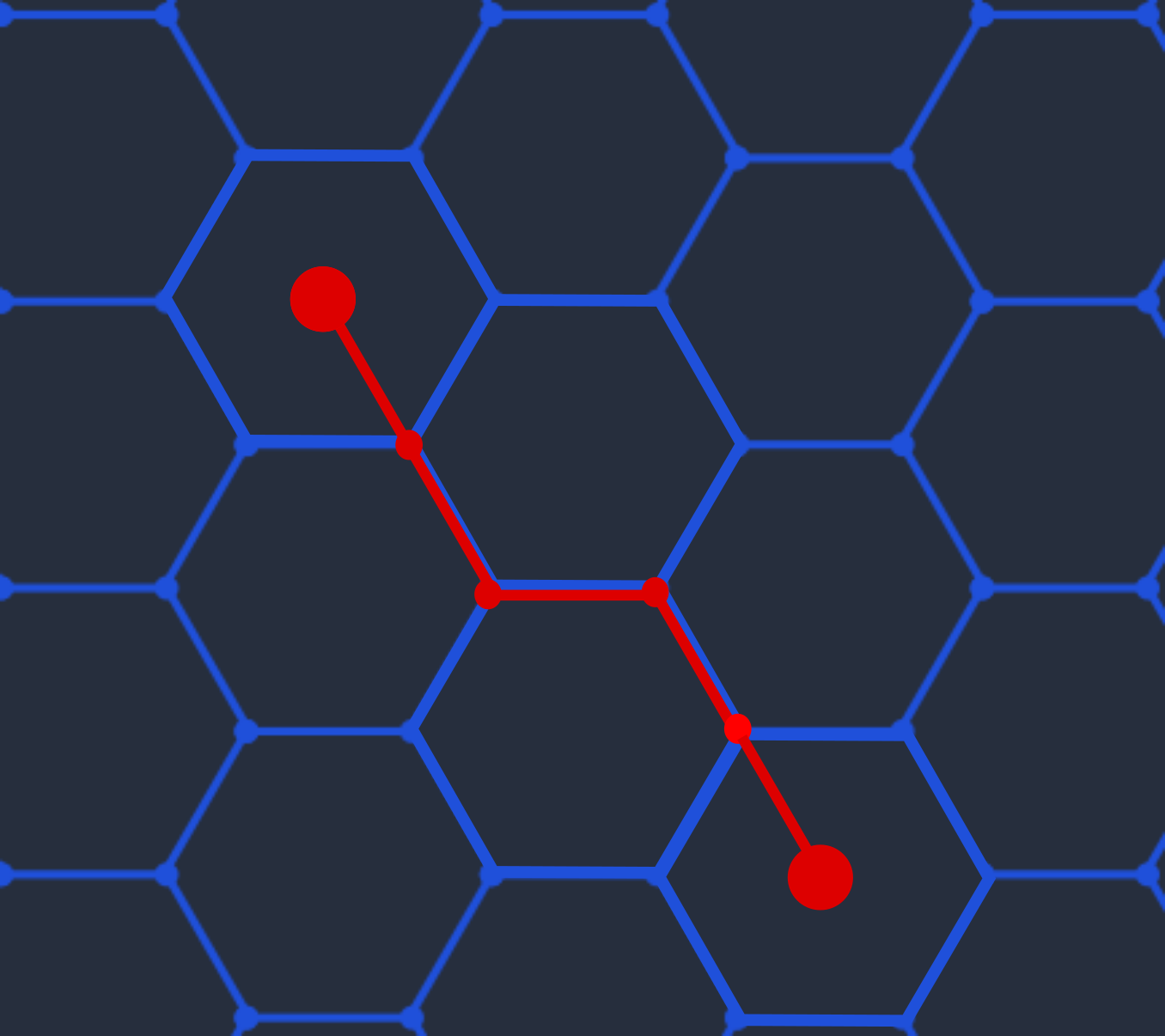
Given p0 is the starting point and p1 is the ending point then create a path as follows:

Add p0 to path.
Let p = p0.
Let h be hexagon at p.

Then repeat:

If h position is the same as p1 position then add p1 to path and stop.
Chose p from vertices h(i) i = {0, 1, 2, 3, 4, 5}, such that dot( h(i) - p0, p1 - p0 ) is maximal.
Add p to path.
Choose the nearest hexagon h from position p using the dot product of nearby hexagon centers and actual position p and direction of p1 - p.

CodePudding user response：

There may be a more efficient algorithm, but this one accomplishes the task.

Calculate the direction from the starting point to the first vertex, in degrees.
```
vi = round( degrees( atan2( Point A, Point B ) ) / 60 )
```
Calculate the angle for the derived vertex.
```
vangle = vi * 60 * pi / 180
```

Calculate the position of the first vertex.

vc = Point A's x   cos( vangle )
vr = Point A's y   sin( vangle )

Determine the next vertex based on the smallest angle of the three possible next vertices with respect to the line of Point A to Point B.
```
start = if vi mod 2 == 1 then -1 else 2
nearest = infinity
```
Loop over the three possible vertices.
```
for k = start step 2 until 3 do
```

Determine the angle between Point B and a candidate vertex.

kangle = k * 60 * pi / 180
nc = vc   cos( kangle )
nr = vr   sin( kangle )

Determine the distance between Point B and the candidate vertex.
```
d = distance( Point B, Point(nc, nr) )
```
If the distance is smaller than any distance found so far, record the vertex and change up the three candidate three vertices (by increasing the selected vertex index):
```
if d < nearest then
  nearest = d
  sc = nc
  sr = nr
  vi = k   1
end
```
Repeat from step 4 until the distance is less than or equal to 1.

Cherry-picked result from this algorithm, with additional modifications:

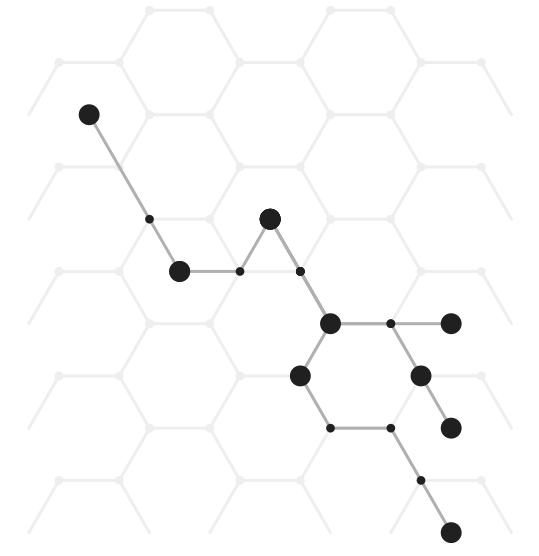
Another result: