I want to implements a simple Task Scheduling. You have a list of tasks that need to be completed. For each task it is known exactly how much time is required for completion (known as "effort") and a task may have a set of dependency task that need to be carried out before it can be started (known as "dependencies"). Given a certain number of available independent workers you have to compute a reasonable task distribution such as

• tasks are not executed before each required task(s) are completed
• there is no idling worker and available task (uncompleted task with 0 uncompleted requirement(s)) at any given time

Example

Given below set of tasks

• Task A requires 1 effort and has 0 depedency
• Task B requires 2 effort and has 0 dependency
• Task C requires 1 effort and depends on A, B

And given 1 worker, the sample execution will be:

Worker ID	Task	Start Time	End Time
1	Task A	0	1
1	Task B	1	3
1	Task C	3	4

And given 2 workers, the sample execution will be:

Worker ID	Task	Start Time	End Time
1	Task A	0	1
2	Task B	0	2
1	Task C	2	3

*A worker can finish a task and pick up a new task at the same time step, refer to the 1st example where Task B start time same as Task A's end time.

*The order of worker and task doesn't matter as long as it fulfills the given requirement.

I also define some API contracts to achieve this

public interface Task extends Iterable<Task> {
    String getName();
    int getEffort();
    List<Task> getDependencies();
}

public interface TaskExecution {
    int getEnd();
    Task getTask();
    int getWorkerId();
    int getStart();
}

public interface Scheduler {
    List<TaskExecution> estimate(Iterable<Task> tasks, int numWorkers);
}

My algorithm is

• Sort the tasks based on their dependencies by using graph
• Allocate workers to sorted tasks and calculate the time

I can do the sort of tasks based on dependencies by using Graph and topological sorting but I am stucked with resource allocation to all tasks so that it can run in parallel if possible.

public class Graph<T> {

  static class Node<E> {
    E source;
    E destination;
    
    Node(E source, E destination) {
      this.source = source;
      this.destination = destination;
    }
  }

  private int vertices;
  private LinkedList<Node<T>>[] adjList;

  public void addEgde(T source, T destination, List<T> list) {
    Node node = new Node(source, destination);
    adjList[list.indexOf(source)].addFirst(node);
  }

  public void topologicalSorting(List<T> list) {
    //....
  }

}

Any idea on how to implement such an worker allocation while having as much parallelism as possible?

CodePudding user response：

In the comments, you mentioned that you were looking for hints, so I'll share some ideas on how to approach the problem. The method I describe is ultimately a greedy algorithm, so it may not be optimal in all cases. It is optimal for the given example, but I would be interested in a counterexample that proves that it's not optimal.

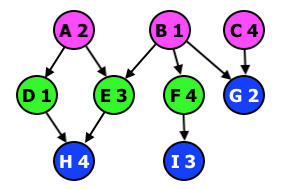
Given the following topological graph, where

• the letter is the task name, and the number is the effort for the task
• purple tasks are starters, they have no dependencies
• green tasks are intermediaries, they depend on other tasks, and tasks depend on them
• blue tasks are terminals, no tasks depend on them

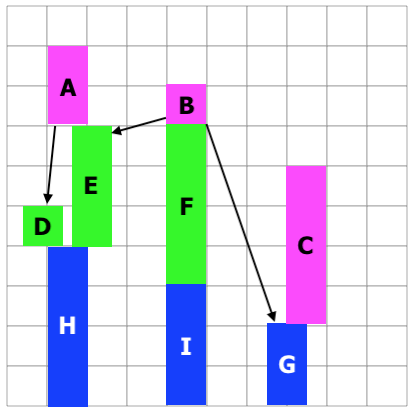
The first step is to convert it (conceptually) to the following task diagram, where

• the letter is the task name
• the height of a task rectangle is proportional to the task effort
• arrows show dependencies that aren't otherwise obvious
• the terminals are aligned so that they all end at the same time
• the end time for non-terminals is as late as possible while meeting the dependency requirements

The conversion from topological graph to task diagram can be done with a breadth-first search. The terminals are assigned a distance of 0, and added to the queue. The edges are reversed, and have a weight equal to the task effort. So for example, there's an edge from "H4" to "D1" with a weight of 4. Tasks aren't added to the queue until all their dependents have been processed. For example, "B1" wouldn't go into the queue until tasks E, F, and G had come out of the queue.

The goal of the conversion is to determine the latest possible start time for each task that would allow all of the terminal tasks to finish at the same time (assuming that an unlimited number of workers were available).

Once every task has been assigned its latest possible starting time, then the greedy algorithm for task assignment begins. For the example, assume that there are two workers available. Then the tasks are assigned as follows:

• A and B are started first.
• F and E are next, but F should start before E since F requires more effort.
• C should be started before D.
• H is before I, and I is before G.

In short, tasks are sorted first by their topological order. Without violating the topological order, tasks are sorted by their start time, and for tasks with the same start time, the task that requires more effort is first.

This can be implemented with a priority queue that sorts based on task start time as the primary key, and task effort as the secondary key. Initially, only the starter tasks are added to the queue. As tasks are pulled from the queue, any tasks whose dependencies have been satisfied are added to the queue.

The final task assignments for the example are:

Worker ID	Task	Start Time	End Time
1	A	0	2
2	B	0	1
2	F	1	5
1	E	2	5
2	C	5	9
1	D	5	6
1	H	6	10
2	I	9	12
1	G	10	12

Note that this is an optimal solution for the example. Both workers finish at time 12. The total amount of effort for the tasks is 24, divided between 2 workers, giving 12 effort from each worker.