CUDA and openCV (CPU) Matrix Addition Performance constant with increasing numels-CodePudding

I compare the performance of Matrix Addition using a simple CPU function, CUDA and openCV (on CPU) by increasing the number of elements consecutively and measuring the runtime. I have plotted the data below. Note that it is one plot per datatype, where CUCV_8U is a macro for unsigned char, CUCV_16U=unsigned short, CUCV32F=float and CUCV64F=double.

I have noticed that the runtime of openCV and CUDA does not increase until the matrices have roughly 2^12 elements. After they exceed that "limit", the runtimes start to diverge (note the logarithmic scaling). Now, I would like to explain that "limit".

If it was only for CUDA, I would suggest it is due to the number of available CUDA cores, which is 1024 for my GTX 960. When the number of total elements in the matrix exceeds the number of cores, the threads can not be executed parallel anymore, but are executed concurrently.

However, openCV seems to follow the same trend (constant runtime until roughly 2^12 elements) and so I am wondering what could be the reason for this. Anyone has an idea?

Thank you!

If you need information about the code I used have a look at my project repo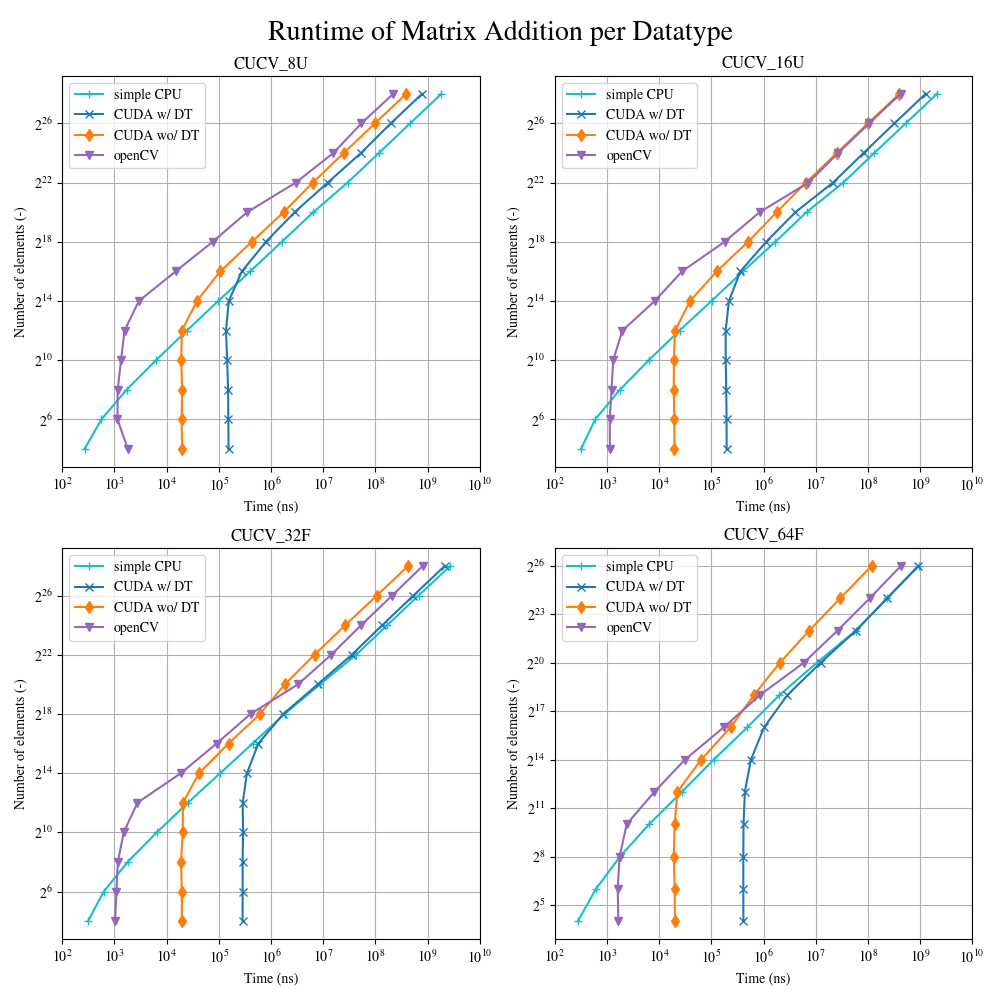

// CUDA Kernel

template <typename T>
__global__ void cuCV::kernel::add(DeviceCuMat<T> OUT, const DeviceCuMat<T> A, const DeviceCuMat<T> B) {
    int col = blockIdx.x * blockDim.x   threadIdx.x;
    int row = blockIdx.y * blockDim.y   threadIdx.y;
    int  ch = blockIdx.z * blockDim.z   threadIdx.z;

    int index = row * A.getWidth()   col   (A.getWidth()*A.getHeight()) * ch;  // linearisation of index

    if (col < A.getWidth() && row < A.getHeight() && ch < A.getNChannels())
        OUT.getDataPtr()[index] = A.getDataPtr()[index]   B.getDataPtr()[index];
}

CodePudding user response：

I have noticed that the runtime of openCV and CUDA does not increase until the matrices have roughly 2^12 elements.

Starting a kernel take some time since it requires an interaction with the OS (more specifically the graphic driver) and the target device with is generally a PCI device (requiring a PCI communication). I/O operations are generally pretty slow and they often has a pretty big latency (for HPC applications). There are many other overheads to consider including the time to allocate data on the device, to manage virtual memory pages, etc. Since system calls tends to takes at least 1 us on most mainstream systems and about dozens of us for the one involving discrete GPUs, the reported timing are expected. The time to start a data transfer to a PCI-based GPU is usually about hundreds of us (at least 10 us on nearly all platforms).

Note that GPUs are designed to execute massively parallel computing code, not low-latency ones. Having more core do not make small computation faster but more operation can be computed faster. This is the principle of the Amdahl's and Gustafson's laws.

If you want to compute small matrices, you should not use a discrete GPU. If you have a lot of them, then you can do that efficiently on a GPU but using one big kernel (not 1 kernel per matrix).

If it was only for CUDA, I would suggest it is due to the number of available CUDA cores, which is 1024 for my GTX 960

Such a computation should not be compute-bound but memory-bound (otherwise, you should clearly optimize the kernel as any GPU should saturate the memory for such basic operation). As a result, what matters is the memory bandwidth of the target GPU, not the number of CUDA core. Also note that the memory of the GPU tends to be faster than the one CPU can use but with a significantly bigger latency.

Also note that the GTX 960 is not design to compute double-precision computation efficiently. In fact, a good mainstream CPU should clearly outperform it for such computation. This GPU is made to speed up simple-precision computation (typically for 3D applications like games). If you want to speed up double-precision computations, then you need a (far more expensive) server-based GPU. Fortunately, this should not be much a problem for memory-bound code.

OpenCV seems to follow the same trend (constant runtime until roughly 2^12 elements)

There are still overhead for the OpenCV implementation. For example creating thread take some time, allocating data too (though it should be significantly faster than on GPU), not to mention caches are certainly cold (so possibly bound by cache misses). The time to create few threads on a mainstream Linux PC is about few us to few dozens of us (generally more on servers due to more core and a more complex architecture).

Overall, the CPU implementation appear to be memory bound since the speed of the computation is dependent of the item size (proportional at first glance). That being said, the throughput appears to be pretty slow if the code assuming the results are for 1 kernel execution (I got 2.5 GiB/s which is pretty bad for a recent mainstream PC). The GPU computation is also suspiciously inefficient since the timings are independent to the item size. This means the computation is certainly not memory-bound and the kernel can likely be optimized (check the layout of the image and the GPU does contiguous access first, and then apply some unrolling so to reduce the overhead of the kernel per thread).

I strongly advise you to profile both the CPU and GPU implementations. The first thing to do for the CPU implementation (for large matrices) is to check whether multiple cores are used and if SIMD instructions are executed. For both the CPU and GPU implementations, you should check the memory throughput.