Using Matplotlib to Plot Sympy Implicit Function-CodePudding

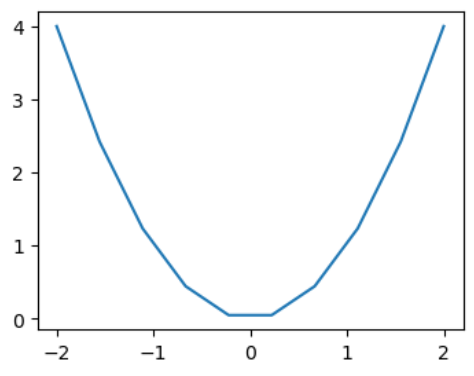
I have an implicit function, say x**2 - y = 0 (to simplify), of which I want to obtain a plot for a certain range of x values.

sympy.plot_implicit usually gives some spreading of the lines that I am not happy with.

I would like to have access to the plotted values, and so pyplot.plot is preferable to me. Usually I use the following piece of code to get my explicit Sympy functions plotted, but I am unsure how to use something similar for exp = sym.Eq(x**2 - y, 0). Does anyone have a solutions for this?

import sympy as sym
import numpy as np
from matplotlib import pyplot as plt

x, y = sym.symbols('x y', nonnegative=True)
exp = x**2

# Plot using a numpy-ready function
x_arr = np.linspace(-2, 2, 100)
exp_func = sym.lambdify(x, exp, 'numpy')
exp_arr = exp_func(x_arr)

plt.plot(x_arr, exp_arr)

PS: my real expression is b_sim (see below) and I want the plot for the equation b_sim = -1. With sym.plot_implicit(b_sim 1, (n,0.225,1.5), (h, -1.1, 1.1)) one can see the lines spreading I dislike. Following Oscar Benjami's tips

CodePudding user response：

To have access to the plotted values of a sympy function plot, in this case the coordinates of lines2d plot, is simple.

Here is the code that plots the function.

import matplotlib.pyplot as plt
from sympy import symbols
import numpy as np
import sympy

x, y = symbols('x y', nonnegative=True)
exp = x**2

# Plot using a numpy-ready function
x_arr = np.linspace(-2, 2, 10)  #small number for demo
exp_func = sympy.lambdify(x, exp, 'numpy')
exp_arr = exp_func(x_arr)

plt.figure(figsize=(4, 3))
lines2d = plt.plot(x_arr, exp_arr)

In the code above, lines2d is a list of line2d objects. To get the coordinates from the 1st (only one in this case), do this:

xys = lines2d[0].get_xydata()

And you can use it to plot with this code:-

fig = plt.figure(figsize=(4, 3))
ax = fig.add_subplot()
ax.plot(xys[:,0], xys[:,1])