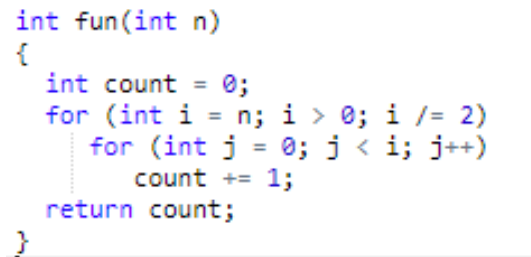
i think that the loops runs o(N) times and wanted to confirmed that and even to expanding knowledge over the steps. Can anyone explain this?

CodePudding user response：

Let k be the least positive number such that 2^k > n.

Observe that your first iteration runs no more than 2^k times. since, n < 2^k, n/2 < 2^{k-1}, hence your second loop runs no more than 2^{k-1} times,
third loop runs 2^{k-2} time, so on and so forth.

Total number of iterations can be upper bounded by 2^k 2^{k-1} .... 2^0 = 2^{k 1}-1.

We assumed that k is the least postive number such that 2^k > n, which implies 2^{k-1} <= n multiplying by 4 on both sides and substracting gives us, 2^{k 1}-1 <= 4n-1

hence total number of iterations is O(n). Although the upper bound 4n-1 is sloppy, it is enough to prove asymtotics. (in reality your loop runs approximately 2n times)