Draw a circle with a specified tilt angle in three-dimensional space with Python-CodePudding

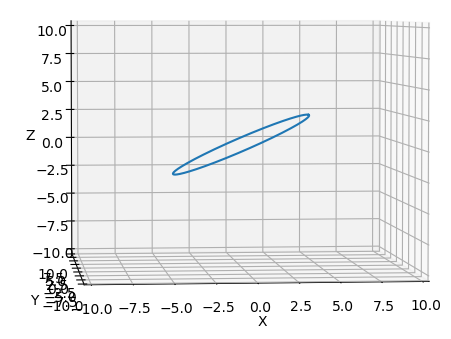
I want to draw a circle with a specified angle of inclination in 3D space using Python. Similar to the image below:

Do the X and Y parts also need to be modified? What should I do?

update: the circle tilt with other axis

CodePudding user response：

Let i = (1, 0, 0), j = (0, 1, 0). Those are the direction vectors of the x-axis and y-axis, respectively. Those two vectors form an orthonormal basis of the horizontal plane. Here "orthonormal" means the two vectors are orthogonal and both have length 1.

A circle on the horizontal plane with centre C and radius r consists in all points that can be written as C r * (cos(theta) * i sin(theta) * j), for all values of theta in range [0, 2 pi]. Note that this works with i and j, but it would have worked equally with any other orthonormal basis of the horizontal plane.

A circle in any other plane can be described exactly the same way, by replacing i and j with two vectors that form an orthonormal basis of that plane.

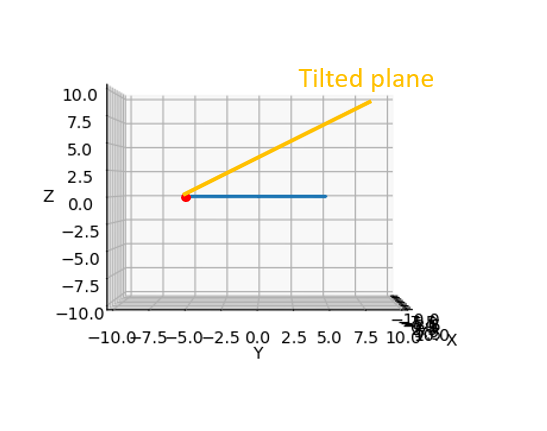
According to your image, the "tilted plane at angle tilt" has the following orthonormal basis:

a = (cos(tilt), 0, sin(tilt))
b = (0, 1, 0)

You can check that these are two vectors in your plane, that they are orthogonal and that they both have norm 1. Thus they are indeed an orthonormal basis of your plane.

Therefore a circle in your plane, with centre C and radius r, can be described as all the points C r * (cos(theta) * a sin(theta) * b), where theta is in range [0, 2 pi].

In terms of x,y,z, this translates into the following system of three parametric equations:

x = x_C   r * cos(theta) * x_a   r * sin(theta) * x_b
y = y_C   r * cos(theta) * y_a   r * sin(theta) * y_b
z = z_C   r * cos(theta) * z_a   r * sin(theta) * z_b

This simplifies a lot, because x_b, y_a, z_b are all equal to 0:

x = x_C   r * cos(theta) * x_a    #   sin(theta) * x_b,  but x_b == 0
y = y_C   r * sin(theta) * y_b    #   cos(theta) * y_a,  but y_a == 0
z = z_C   r * cos(theta) * z_a    #   sin(theta) * z_b,  but z_b == 0

Replacing x_a, y_b and z_a by their values:

x = x_C   r * cos(tilt) * cos(theta)
y = y_C   r * sin(theta)
z = z_C   r * sin(tilt) * cos(theta)

In python:

import numpy as np
import matplotlib.pyplot as plt

# parameters of circle
r = 5.0                         # radius
x_C, y_C, z_C = (0.0, 0.0, 0.0) # centre
tilt = np.pi / 6                # tilt of plane around y-axis

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_xlim(-10,10)
ax.set_ylim(-10,10)
ax.set_zlim(-10,10)

theta = np.linspace(0, 2 * np.pi, 300) #to make a full circle

x = x_C   r * np.cos(tilt) * np.cos(theta)
y = y_C   r * np.sin(theta)
z = z_C   r * np.sin(tilt) * np.cos(theta)

ax.plot(x, y, z )
plt.show()