How do I plot this piecewise function into Python with matplotlib?-CodePudding

This is the function I need to plot:

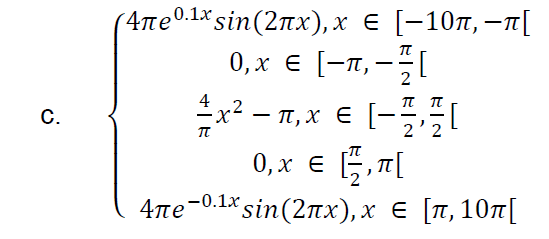
This is my code:

pi = np.pi
sin = np.sin
e = np.e

x1 = np.linspace(-10*pi, -pi)
y1 = (4*pi*(e**0.1*x1)) * sin(2*pi*x1)
plt.plot(x1, y1)

x2 = np.linspace(-pi, -pi/2)
y2 = 0
plt.plot(x2, y2)

x3 = np.linspace(-pi/2, pi/2)
y3 = 4/pi * x3**2 - pi
plt.plot(x3, y3)

x4 = np.linspace(pi/2, pi)
y4 = 0
plt.plot(x4, y4)

plt.show()

But every time I try to run it gives me a ValueError:

ValueError: x and y must have same first dimension, but have shapes (50,) and (1,)

I have tried using np.piecewise but haven't gotten anywhere.

CodePudding user response：

I usually use a chained sequence of numpy.where to define a piecewise function.
First, the domain for the independent variable, then the conditions and the analytical expression, with a difference for the last where, as explained in the docs.
NB: are you sure that the circular frequency of the sines is 2π? when I see a domain expressed in multiples of π I think immediately to frequencies expressed as integer numbers or simple fractions…

from numpy import exp,linspace, pi, sin, where
from matplotlib.pyplot import grid, plot, show

x = linspace(-10*pi,  10*p, 2001)
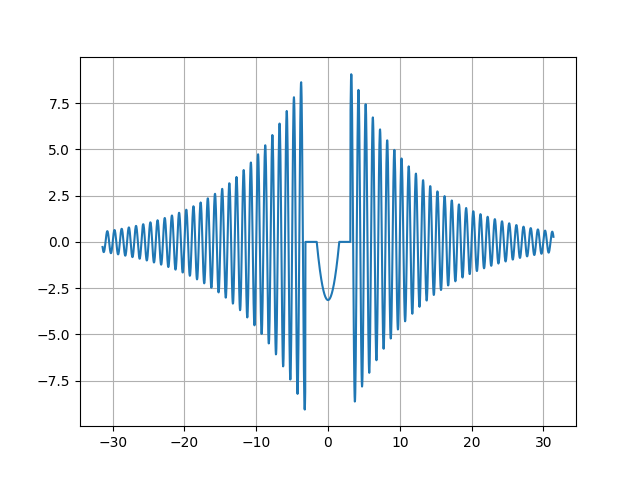
y = where(x <  -pi, 4*pi*exp( x/10)*sin(2*pi*x),
    where(x <-pi/2, 0,
    where(x < pi/2, 4*x*x/pi-pi,
    where(x <   pi, 0, 4*pi*exp(-x/10)*sin(2*pi*x)))))
    
plot(x, y) ; grid() ; show()

CodePudding user response：

x2 is an array, and y2 is a number, matplotlib expects both to be arrays, so you should switch y2 and y4 definition to be y2 = np.zeros_like(x2), and y4 = np.zeros_like(x4).

CodePudding user response：

As x and y need to be the same first dimension, you might want to define y2 and y4 to be a function of x, so that an array of the same dimension is produced as a result to plot.

#...
y2 = x2*0
plt.plot(x2, y2)

#...

y4 = x4*0
plt.plot(x4, y4)

Alternatively, you could have y2 and y4 defined as an array of zeros of the same size of x2 and x4 respectively.

y2 = np.zeros(x2.shape)
y4 = np.zeros(x4.shape)