I am trying to create a simple path system with C# in Unity.

So far, everything works perfectly. But to create a path follower, I need the position to which the follower should move every frame. The paths always have a radius, a starting point and a length, the rest is unknown.

Now, how do I calculate the position of the path follower in each frame, i.e. point on the arc? I need a function that takes as argument the percentage position of the follower on the path and that returns a global position in the scene. Here is an example: the length of the arc L, the radius r and the starting point A are given. What I am trying to calculate is the random point D:

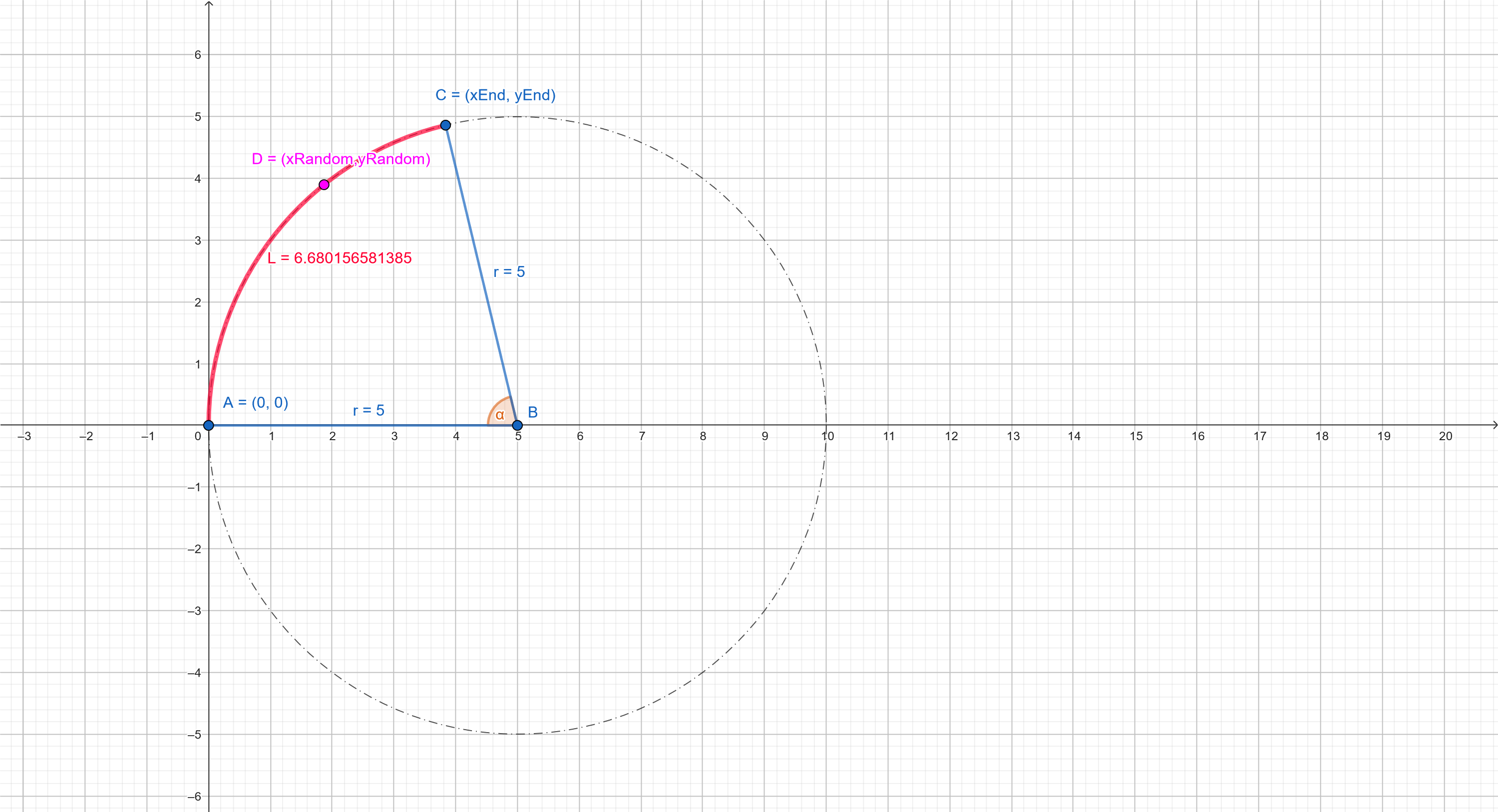
The point that I calculate on my own is just a mess and doesn't work, even though I've already done some research. So I am looking for a simple and understandable solution.

CodePudding user response：

Percentage is between 0 and 1 and Length is the arc length.

 Vector3 getPoint(Vector3 start, float length, float radius, float percentage){
        
        float end = length / radius * (Mathf.PI / 180f);
        float angle = end * percentage;

        float x = start.x - radius   Mathf.Cos(angle) * radius;
        float y = start.y - radius   Mathf.Sin(angle) * radius;
        float z = start.z;

        return new Vector3(x, y, z);
    }

CodePudding user response：

the length of the arc L, the radius r and the starting point A are given

• A circles circumference is defined by 2 * r * pi. A whole circumference, calculated using r=5: fullCircumference = 31.4159265359.
• A partical circumference (the arc) is given by L, we know it's L/fullCircumference gives 0.21263598811 which is the fraction that L takes from the whole circumference.
• We can convert the arc fraction to radians, given that a whole circle has 2PI -> 0.21263598811 * 2 * PI = 1.33603131627 rad
• Now to the Starting Point A. I assume it's always ON the arc somewhere. Though, if we start with sin(0) and cos(0) we are at "12 o Clock": 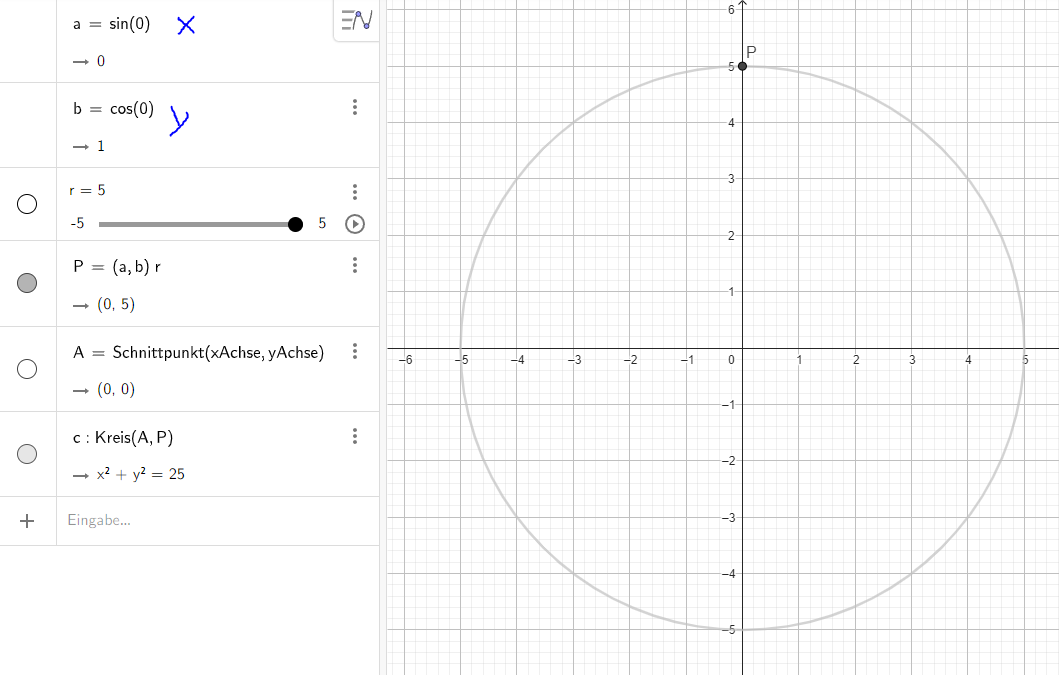So we need to calculate the offset in radians around the circle.
• Though you didn't give us B and I can't assume that though the radius alone. So I will just ignore this for now and offset the forumla by 90° (or half pi) to get to A
• D's x & y would then be defined by: D(sin(x - pi/2) * r, cos(x - pi/2)) * r;
• And if we enter the 1.336 rad we calculated, it looks about right:

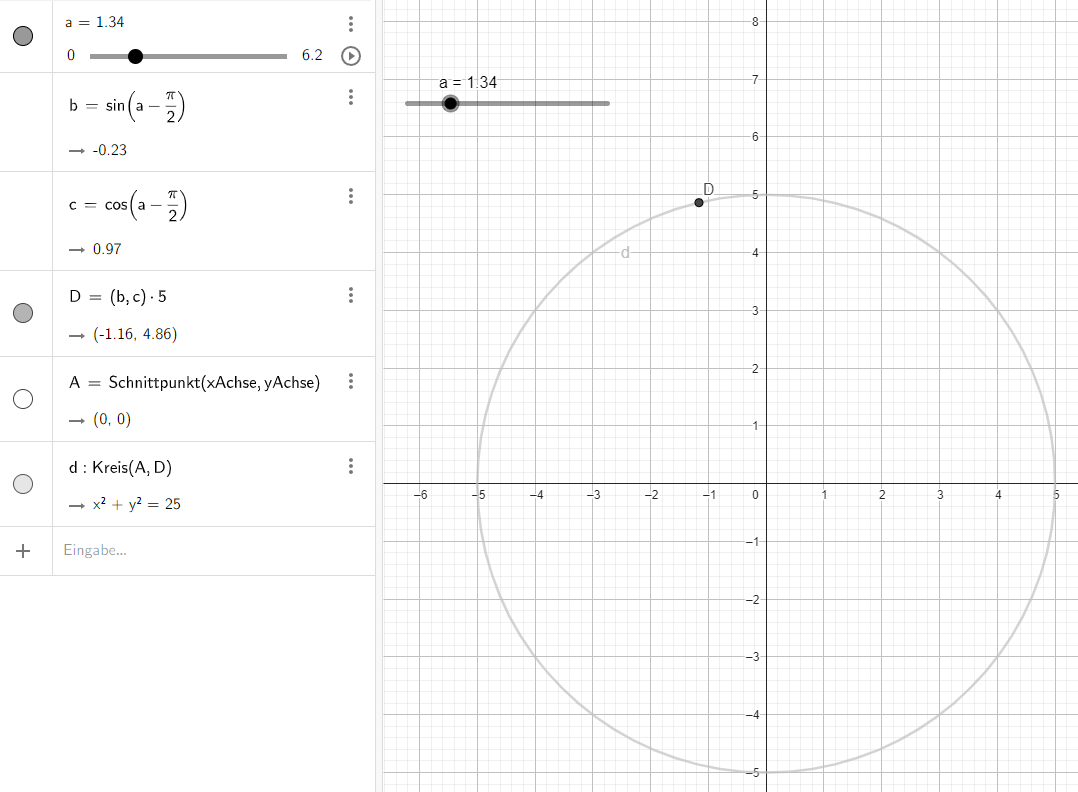
The c# code would look like this (didn't compile though):

 Vector2 pointOnCircle(float L, float r){
    
    float fullCircumference = 2f * Mathf.PI * r;
    float partialCircumference = L / fullCircumference;
    float arcRadians = partialCircumference * 2f * Mathf.PI;

    float circularOffset = Mathf.PI / 2f;
    Vector2 D = new Vector2();
    D.x = Mathf.Sin(arcRadians - circularOffset) * r;
    D.y = Mathf.Cos(arcRadians - circularOffset) * r;

    return D;
}

• So we got C, now you want a random point D between A and C on that arc.
• We now need to sample a point on the arc using a fraction between 0 and 1 (0 being at A, 1 being at C):
• The arc's length is arcRadians in radians, so we can just mutiply that with 0..1:

code:

Vector2 pointOnArc(float L, float r, float fraction){ // fraction is between 0 and 1
    
    float fullCircumference = 2f * Mathf.PI * r;
    float partialCircumference = L / fullCircumference;
    float arcRadians = partialCircumference * 2f * Mathf.PI;

    float circularOffset = Mathf.PI / 2f;
    Vector2 D = new Vector2();
    D.x = Mathf.Sin(fraction * arcRadians - circularOffset) * r;
    D.y = Mathf.Cos(fraction * arcRadians - circularOffset) * r;

    return D;
}

And there you go: