which type of algorithm suits the best to find the most similar molecule with respect to the actual-CodePudding

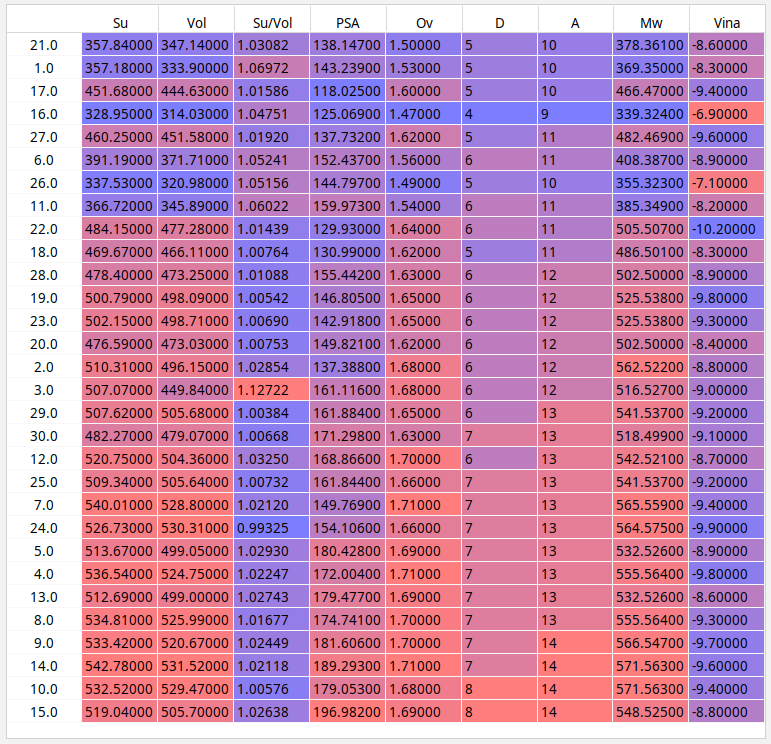
The data consists of some properties of drug candidate molecules (the last row is the actual drug)

Mol= Molecule name, Su= Surface area, Vol= Volume, PSA= Polar Surface Area, Ov = Ovality, D = HB donating group, A = HB acceptors, Mw = Molecular weight, Vina = binding affinity to the protein.

I have tried scipy.spatial.distance.cdist library to sort them from the most similar to the least with respect to the actual drug. but there are a lot of different algorithms, which lead to different results. I was wondering which method is the best for this case.

import scipy.spatial
ary = scipy.spatial.distance.cdist(df2, df1, metric='correlation')
df2[ary==ary.min()]

the outcome will be molecule number 2.

import scipy.spatial
ary = scipy.spatial.distance.cdist(df2, df1, metric='correlation')
df2[ary==ary.min()]

the outcome will be molecule number 16.

and besides that how can I make this calculation weighted? I mean making some factors more important and some less. (and How to visualize that)

    Mol   Su     Vol        Su/Vol  PSA      Ov     D   A     Mw    Vina

 1.  1  357.18  333.9   1.069721473 143.239 1.53    5   10  369.35  -8.3
 2.  2  510.31  496.15  1.028539756 137.388 1.68    6   12  562.522 -8.8
 3.  3  507.07  449.84  1.127223013 161.116 1.68    6   12  516.527 -9.0
 4.  4  536.54  524.75  1.022467842 172.004 1.71    7   13  555.564 -9.8
 5.  5  513.67  499.05  1.029295662 180.428 1.69    7   13  532.526 -8.9
 6.  6  391.19  371.71  1.052406446 152.437 1.56    6   11  408.387 -8.9
 7.  7  540.01  528.8   1.021198941 149.769 1.71    7   13  565.559 -9.4
 8.  8  534.81  525.99  1.01676838  174.741 1.7     7   13  555.564 -9.3
 9.  9  533.42  520.67  1.024487679 181.606 1.7     7   14  566.547 -9.7
 10. 10 532.52  529.47  1.005760477 179.053 1.68    8   14  571.563 -9.4
 11. 11 366.72  345.89  1.060221458 159.973 1.54    6   11  385.349 -8.2
 12. 12 520.75  504.36  1.032496629 168.866 1.7     6   13  542.521 -8.7
 13. 13 512.69  499     1.02743487  179.477 1.69    7   13  532.526-8.6
 14. 14 542.78  531.52  1.021184527 189.293 1.71    7   14  571.563 -9.6
 15. 15 519.04  505.7   1.026379276 196.982 1.69    8   14  548.525 -8.8
 16. 16 328.95  314.03  1.047511384 125.069 1.47    4   9   339.324 -6.9
 17. 17 451.68  444.63  1.01585588  118.025 1.6     5   10  466.47  -9.4
 18. 18 469.67  466.11  1.007637682 130.99  1.62    5   11  486.501 -8.3
 19. 19 500.79  498.09  1.005420707 146.805 1.65    6   12  525.538 -9.8
 20. 20 476.59  473.03  1.00752595  149.821 1.62    6   12  502.5   -8.4
 21. 21 357.84  347.14  1.030823299 138.147 1.5     5   10  378.361 -8.6
 22. 22 484.15  477.28  1.014394066 129.93  1.64    6   11  505.507 -10.2
 23. 23 502.15  498.71  1.006897796 142.918 1.65    6   12  525.538 -9.3
 24. 24 526.73  530.31  0.993249232 154.106 1.66    7   13  564.575 -9.9
 25. 25 509.34  505.64  1.007317459 161.844 1.66    7   13  541.537 -9.2
 26. 26 337.53  320.98  1.051560845 144.797 1.49    5   10  355.323 -7.1
 27. 27 460.25  451.58  1.019199256 137.732 1.62    5   11  482.469 -9.6
 28. 28 478.4   473.25  1.010882198 155.442 1.63    6   12  502.5   -8.9
 29. 29 507.62  505.68  1.003836418 161.884 1.65    6   13  541.537 -9.2
 30. 30 482.27  479.07  1.006679608 171.298 1.63    7   13  518.499 -9.1
 31.V0L 355.19  333.42  1.065293024 59.105  1.530   0   9   345.37  -10.4

CodePudding user response：

which method is the best for this case

My favourite colour is orange. Pick one that's orange-coloured. Orange is best. You need to offer much, much, much more specific criteria. An approach that is

fairly unsurprising,
simple,
fast, and
well-suited to later weight scaling

is for you to scale all of your variables to a unit normal distribution and then apply a Euclidean (Frobenius) norm:

from io import StringIO

import numpy as np
import pandas as pd

content = \
'''
Idx Mol Su      Vol     Su/Vol      PSA     Ov      D   A   Mw      Vina
1.   1  357.18  333.9   1.069721473 143.239 1.53    5   10  369.35  -8.3
2.   2  510.31  496.15  1.028539756 137.388 1.68    6   12  562.522 -8.8
3.   3  507.07  449.84  1.127223013 161.116 1.68    6   12  516.527 -9.0
4.   4  536.54  524.75  1.022467842 172.004 1.71    7   13  555.564 -9.8
5.   5  513.67  499.05  1.029295662 180.428 1.69    7   13  532.526 -8.9
6.   6  391.19  371.71  1.052406446 152.437 1.56    6   11  408.387 -8.9
7.   7  540.01  528.8   1.021198941 149.769 1.71    7   13  565.559 -9.4
8.   8  534.81  525.99  1.01676838  174.741 1.7     7   13  555.564 -9.3
9.   9  533.42  520.67  1.024487679 181.606 1.7     7   14  566.547 -9.7
10.  10 532.52  529.47  1.005760477 179.053 1.68    8   14  571.563 -9.4
11.  11 366.72  345.89  1.060221458 159.973 1.54    6   11  385.349 -8.2
12.  12 520.75  504.36  1.032496629 168.866 1.7     6   13  542.521 -8.7
13.  13 512.69  499     1.02743487  179.477 1.69    7   13  532.526 -8.6
14.  14 542.78  531.52  1.021184527 189.293 1.71    7   14  571.563 -9.6
15.  15 519.04  505.7   1.026379276 196.982 1.69    8   14  548.525 -8.8
16.  16 328.95  314.03  1.047511384 125.069 1.47    4   9   339.324 -6.9
17.  17 451.68  444.63  1.01585588  118.025 1.6     5   10  466.47  -9.4
18.  18 469.67  466.11  1.007637682 130.99  1.62    5   11  486.501 -8.3
19.  19 500.79  498.09  1.005420707 146.805 1.65    6   12  525.538 -9.8
20.  20 476.59  473.03  1.00752595  149.821 1.62    6   12  502.5   -8.4
21.  21 357.84  347.14  1.030823299 138.147 1.5     5   10  378.361 -8.6
22.  22 484.15  477.28  1.014394066 129.93  1.64    6   11  505.507 -10.2
23.  23 502.15  498.71  1.006897796 142.918 1.65    6   12  525.538 -9.3
24.  24 526.73  530.31  0.993249232 154.106 1.66    7   13  564.575 -9.9
25.  25 509.34  505.64  1.007317459 161.844 1.66    7   13  541.537 -9.2
26.  26 337.53  320.98  1.051560845 144.797 1.49    5   10  355.323 -7.1
27.  27 460.25  451.58  1.019199256 137.732 1.62    5   11  482.469 -9.6
28.  28 478.4   473.25  1.010882198 155.442 1.63    6   12  502.5   -8.9
29.  29 507.62  505.68  1.003836418 161.884 1.65    6   13  541.537 -9.2
30.  30 482.27  479.07  1.006679608 171.298 1.63    7   13  518.499 -9.1
31. V0L 355.19  333.42  1.065293024 59.105  1.530   0   9   345.37  -10.4
'''

with StringIO(content) as f:
    df = pd.read_fwf(f).set_index('Idx').iloc[:, 1:]

normal = (df - df.mean()) / df.std()
ref = normal.iloc[-1, :]
dist = np.linalg.norm(normal.iloc[:-1, :].values - ref.values, axis=1)
order = np.argsort(dist)
ordered = df.iloc[order, :]

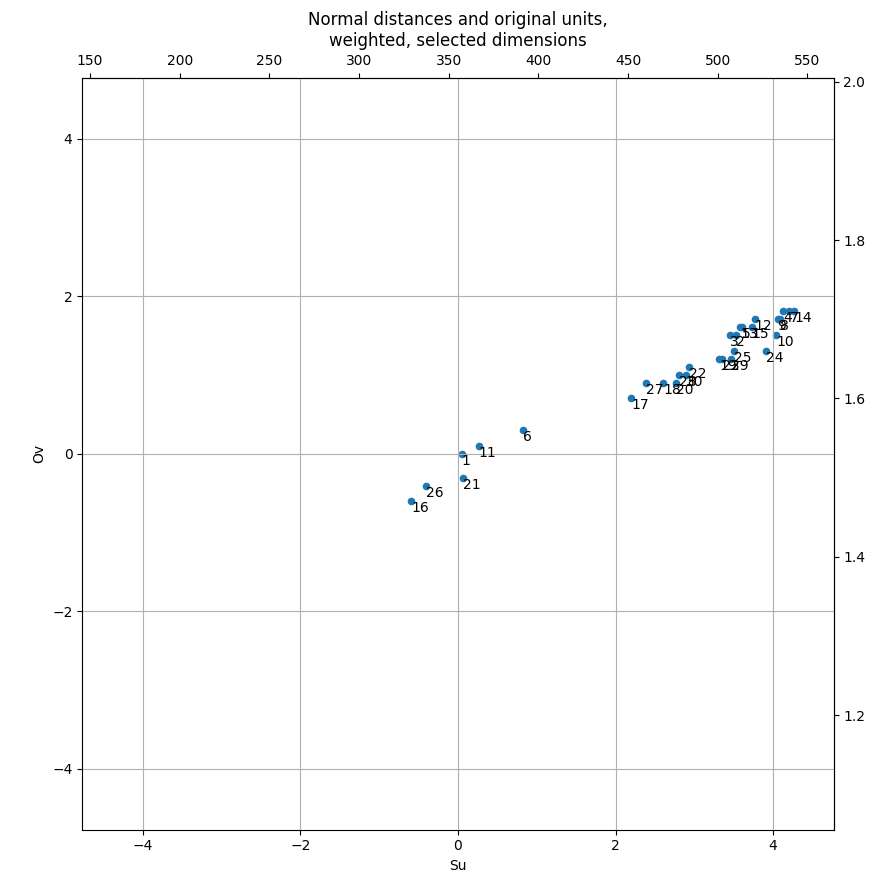
To apply and visualise weights: you have high-dimensional data so you can't practically visualise everything at once; the simplest thing to do is choose two interesting dimensions and plot them. Make for absolute sure that your horizontal and vertical axis scales are identical.

from io import StringIO

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

content = \
'''
Mol Su      Vol     Su/Vol      PSA     Ov      D   A   Mw      Vina
 1  357.18  333.9   1.069721473 143.239 1.53    5   10  369.35  -8.3
 2  510.31  496.15  1.028539756 137.388 1.68    6   12  562.522 -8.8
 3  507.07  449.84  1.127223013 161.116 1.68    6   12  516.527 -9.0
 4  536.54  524.75  1.022467842 172.004 1.71    7   13  555.564 -9.8
 5  513.67  499.05  1.029295662 180.428 1.69    7   13  532.526 -8.9
 6  391.19  371.71  1.052406446 152.437 1.56    6   11  408.387 -8.9
 7  540.01  528.8   1.021198941 149.769 1.71    7   13  565.559 -9.4
 8  534.81  525.99  1.01676838  174.741 1.7     7   13  555.564 -9.3
 9  533.42  520.67  1.024487679 181.606 1.7     7   14  566.547 -9.7
 10 532.52  529.47  1.005760477 179.053 1.68    8   14  571.563 -9.4
 11 366.72  345.89  1.060221458 159.973 1.54    6   11  385.349 -8.2
 12 520.75  504.36  1.032496629 168.866 1.7     6   13  542.521 -8.7
 13 512.69  499     1.02743487  179.477 1.69    7   13  532.526 -8.6
 14 542.78  531.52  1.021184527 189.293 1.71    7   14  571.563 -9.6
 15 519.04  505.7   1.026379276 196.982 1.69    8   14  548.525 -8.8
 16 328.95  314.03  1.047511384 125.069 1.47    4   9   339.324 -6.9
 17 451.68  444.63  1.01585588  118.025 1.6     5   10  466.47  -9.4
 18 469.67  466.11  1.007637682 130.99  1.62    5   11  486.501 -8.3
 19 500.79  498.09  1.005420707 146.805 1.65    6   12  525.538 -9.8
 20 476.59  473.03  1.00752595  149.821 1.62    6   12  502.5   -8.4
 21 357.84  347.14  1.030823299 138.147 1.5     5   10  378.361 -8.6
 22 484.15  477.28  1.014394066 129.93  1.64    6   11  505.507 -10.2
 23 502.15  498.71  1.006897796 142.918 1.65    6   12  525.538 -9.3
 24 526.73  530.31  0.993249232 154.106 1.66    7   13  564.575 -9.9
 25 509.34  505.64  1.007317459 161.844 1.66    7   13  541.537 -9.2
 26 337.53  320.98  1.051560845 144.797 1.49    5   10  355.323 -7.1
 27 460.25  451.58  1.019199256 137.732 1.62    5   11  482.469 -9.6
 28 478.4   473.25  1.010882198 155.442 1.63    6   12  502.5   -8.9
 29 507.62  505.68  1.003836418 161.884 1.65    6   13  541.537 -9.2
 30 482.27  479.07  1.006679608 171.298 1.63    7   13  518.499 -9.1
V0L 355.19  333.42  1.065293024 59.105  1.530   0   9   345.37  -10.4
'''

with StringIO(content) as f:
    df = pd.read_fwf(f).set_index('Mol')

# Higher weight means that more distant values have a more adverse effect on proximity
weights = pd.Series({
    'Su': 1.5,
    'Vol': 1,
    'Su/Vol': 1,
    'PSA': 1,
    'Ov': 0.7,
    'D': 1,
    'A': 1,
    'Mw': 1,
    'Vina': 1,
})

samples = df.iloc[:-1, :]
mean = samples.mean()
std = samples.std()
normal = (samples - mean) / std
ref = (df.loc['V0L', :] - mean) / std
deltas = (normal - ref)*weights
dist = np.linalg.norm(deltas.values, axis=1)
order = np.argsort(dist)
ordered = df.iloc[order, :]

edge = max(-deltas.Su.min(), -deltas.Ov.min(),
            deltas.Su.max(),  deltas.Ov.max())   0.5
lims = (-edge, edge)

fig, ax = plt.subplots(subplot_kw={'aspect': 'equal'})
deltas.plot(
    x='Su', y='Ov', kind='scatter', ax=ax,
    xlim=lims, ylim=lims, grid=True,
    title='Normal distances and original units,\nweighted, selected dimensions'
)
us = df.iloc[:-1, :][['Su', 'Ov']]
ax.secondary_xaxis(location='top', functions=(
    lambda x: (x/weights.Su   ref.Su)*std.Su   mean.Su,
    lambda x: ((x - mean.Su)/std.Su - ref.Su) * weights.Su,
))
ax.secondary_yaxis(location='right', functions=(
    lambda y: (y/weights.Ov   ref.Ov)*std.Ov   mean.Ov,
    lambda y: ((y - mean.Ov)/std.Ov - ref.Ov) * weights.Ov,
))

for name, row in deltas.iterrows():
    ax.text(
        x=row.Su, y=row.Ov, s=name,
        va='top', ha='left',
    )

plt.show()