Check Whether my Plot of Bounded Region and Its Revolution toward x-axis and toward y-axis are corre-CodePudding

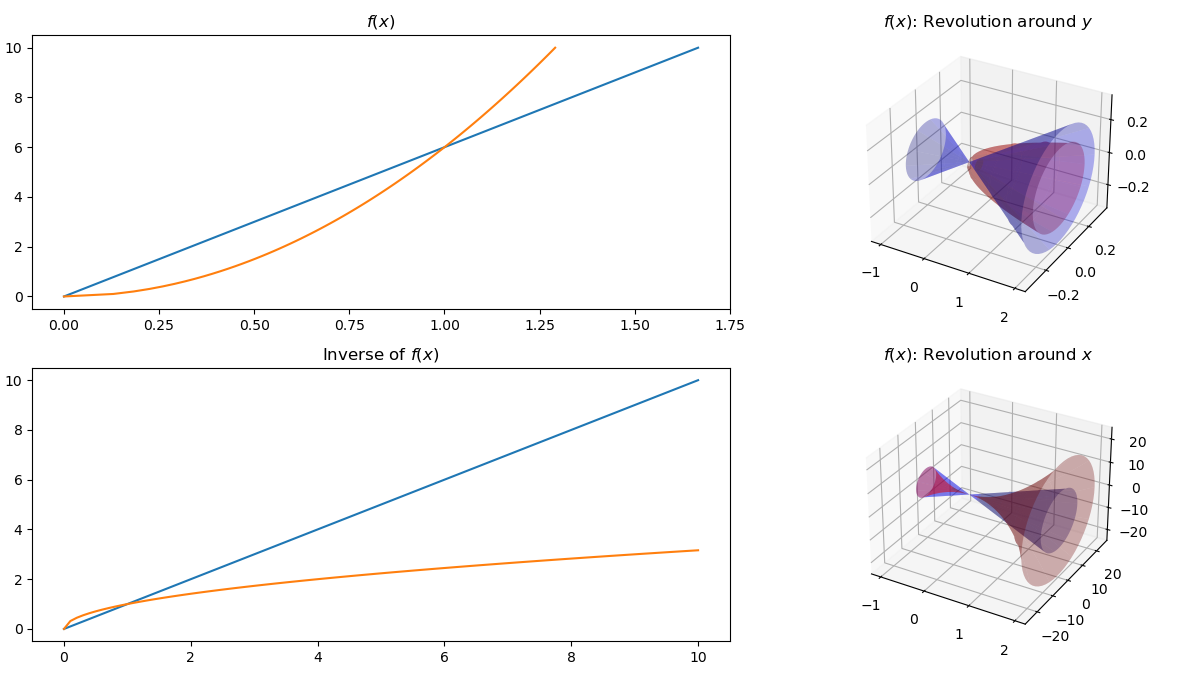
I have tried this code to be able to plot a bounded region, between y=6x and y= 6x^{2}

Please check whether it is correct or not...

I want the bounded region to be revolved around x axis and y axis, become solid of revolution.
I want to add a legend so people will know the blue line is y=6x and the orange line is y=6x^{2}

this is my MWE:

# Compare the plot at xy axis with the solid of revolution toward x and y axis
# For region bounded by the line y = 6x and y = 6x^2
import matplotlib.pyplot as plt
import numpy as np

n = 100

fig = plt.figure(figsize=(14, 7))
ax1 = fig.add_subplot(221)
ax2 = fig.add_subplot(222, projection='3d')
ax3 = fig.add_subplot(223)
ax4 = fig.add_subplot(224, projection='3d')

y = np.linspace(0, 10, n)
x1 = (y/6) 
x2 = (y/6) ** (1/2)
t = np.linspace(0, np.pi * 2, n)

u = np.linspace(-1, 2, 60)
v = np.linspace(0, 2*np.pi, 60)
U, V = np.meshgrid(u, v)

X = U
Y1 = (6*U**2)*np.cos(V)
Z1 = (6*U**2)*np.sin(V)

Y2 = (6*U)*np.cos(V)
Z2 = (6*U)*np.sin(V)

Y3 = ((1/6)*U**(1/2))*np.cos(V)
Z3 = ((1/6)*U**(1/2))*np.sin(V)

Y4 = (U/6)*np.cos(V)
Z4 = (U/6)*np.sin(V)

xn = np.outer(x1, np.cos(t))
yn = np.outer(x1, np.sin(t))
zn = np.zeros_like(xn)
for i in range(len(x1)):
    zn[i:i   1, :] = np.full_like(zn[0, :], y[i])

ax1.plot(x1, y, x2, y)
ax1.set_title("$f(x)$")
ax2.plot_surface(X, Y3, Z3, alpha=0.3, color='red', rstride=6, cstride=12)
ax2.plot_surface(X, Y4, Z4, alpha=0.3, color='blue', rstride=6, cstride=12)
ax2.set_title("$f(x)$: Revolution around $y$")

# find the inverse of the function
x_inverse = y
y1_inverse = np.power(x_inverse, 1)
y2_inverse = np.power(x_inverse, 1 / 2)

ax3.plot(x_inverse, y1_inverse, x_inverse, y2_inverse)
ax3.set_title("Inverse of $f(x)$")


ax4.plot_surface(X, Y1, Z1, alpha=0.3, color='red', rstride=6, cstride=12)
ax4.plot_surface(X, Y2, Z2, alpha=0.3, color='blue', rstride=6, cstride=12)
ax4.set_title("$f(x)$: Revolution around $x$")

plt.tight_layout()
plt.show()

CodePudding user response：

The blue line in your bottom left figure is y = x instead of the inverse of y = 6x...

I changed it to y = 1/6x.

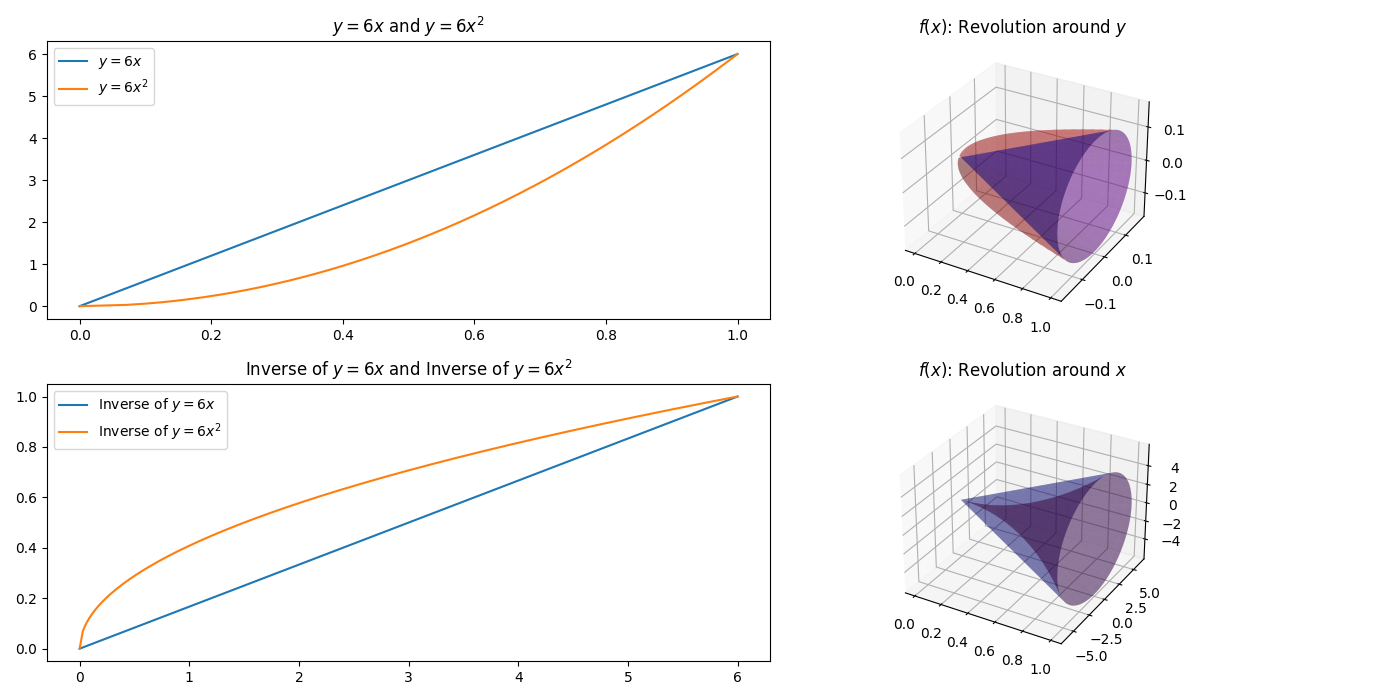
Plotting the revolution of the bounded region can be done by limiting the np.linspace of the y, u, and x_inverse values in your code. You can determine the limits by finding the intersection points of the two functions.

In the upper left plot, they intersect at (0, 0) and (1, 6).

In the bottom left plot, they intersect at (0, 0) and (6, 1).

The legends are also added. See the complete code below.

What I changed:

n = 200
y = np.linspace(0, 6, n)
u = np.linspace(0, 1, n)
v = np.linspace(0, 2*np.pi, n)
x_inverse = np.linspace(0, 6, n)
y1_inverse = np.power(x_inverse/6, 1)
y2_inverse = np.power(x_inverse/6, 1 / 2)

Complete code:

# Compare the plot at xy axis with the solid of revolution toward x and y axis
# For region bounded by the line y = 6x and y = 6x^2
import matplotlib.pyplot as plt
import numpy as np

n = 200

fig = plt.figure(figsize=(14, 7))
ax1 = fig.add_subplot(221)
ax2 = fig.add_subplot(222, projection='3d')
ax3 = fig.add_subplot(223)
ax4 = fig.add_subplot(224, projection='3d')

y = np.linspace(0, 6, n)
x1 = (y / 6)
x2 = (y / 6) ** (1 / 2)
t = np.linspace(0, np.pi * 2, n)

u = np.linspace(0, 1, n)
v = np.linspace(0, 2 * np.pi, n)
U, V = np.meshgrid(u, v)

X = U
Y1 = (6 * U ** 2) * np.cos(V)
Z1 = (6 * U ** 2) * np.sin(V)

Y2 = (6 * U) * np.cos(V)
Z2 = (6 * U) * np.sin(V)

Y3 = ((1 / 6) * U ** (1 / 2)) * np.cos(V)
Z3 = ((1 / 6) * U ** (1 / 2)) * np.sin(V)

Y4 = (U / 6) * np.cos(V)
Z4 = (U / 6) * np.sin(V)

xn = np.outer(x1, np.cos(t))
yn = np.outer(x1, np.sin(t))
zn = np.zeros_like(xn)
for i in range(len(x1)):
    zn[i:i   1, :] = np.full_like(zn[0, :], y[i])

ax1.plot(x1, y, label='$y=6x$')
ax1.plot(x2, y, label='$y=6x^{2}$')
ax1.legend()

ax1.set_title('$y=6x$ and $y=6x^{2}$')
ax2.plot_surface(X, Y3, Z3, alpha=0.3, color='red', rstride=6, cstride=12)
ax2.plot_surface(X, Y4, Z4, alpha=0.3, color='blue', rstride=6, cstride=12)
ax2.set_title("$f(x)$: Revolution around $y$")

# find the inverse of the function
x_inverse = np.linspace(0, 6, n)
y1_inverse = np.power(x_inverse/6, 1)
y2_inverse = np.power(x_inverse/6, 1 / 2)

ax3.plot(x_inverse, y1_inverse, label='Inverse of $y=6x$')
ax3.plot(x_inverse, y2_inverse, label='Inverse of $y=6x^{2}$')
ax3.set_title('Inverse of $y=6x$ and Inverse of $y=6x^{2}$')
ax3.legend()


ax4.plot_surface(X, Y1, Z1, alpha=0.3, color='red', rstride=6, cstride=12)
ax4.plot_surface(X, Y2, Z2, alpha=0.3, color='blue', rstride=6, cstride=12)
ax4.set_title("$f(x)$: Revolution around $x$")

plt.tight_layout()
plt.show()