Plotting arrows perpendicular to coordinates-CodePudding

I have a plot like this, plotting a semicircle with x and y

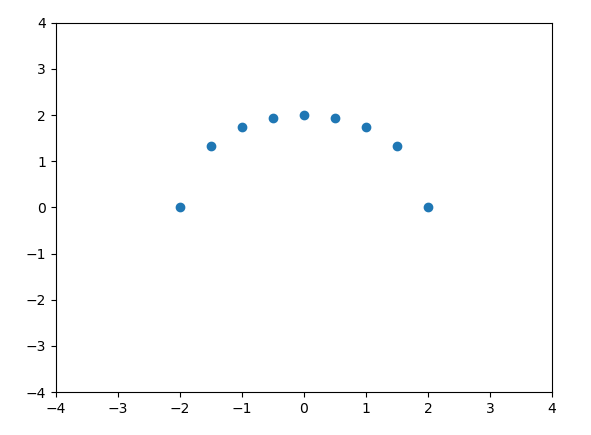
I want to add arrows at each point like so (ignore the horrible paint job):

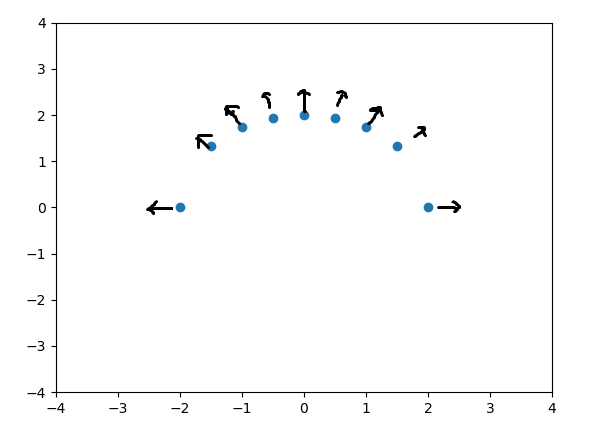
Is there an easy way to add arrows perpendicular to the plot?

Current code:

import numpy as np
import matplotlib.pyplot as plt

r = 2
h = 0
k = 0

x0 = h-r
x1 = h r

x = np.linspace(x0,x1,9)
y = k   np.sqrt(r**2 - (x-h)**2)

plt.scatter(x,y)
plt.xlim(-4,4)
plt.ylim(-4,4)

CodePudding user response：

A point in space has no idea what "perpendicular" means, but assuming your y is some function of x that has a derivate, you can think of the derivate of the function at some point to be the tangent of the curve at that point, and to get a perpendicular vector you just need to rotate the vector counter-clockwise 90 degrees:

x1, y1 = -y0, x0

CodePudding user response：

We know that these points come from a circle. So given three points we can easily find the center using basic geometry notions. If you need a refresher, take a look

If you are in a hurry and you do not have time to implement equations, you could use the

That is the main advantage of this solution over blunova's: it is your code, essentially. And would work if you change f, without assuming that f is a circle. All that is assume is that f is derivable (and if it were not, you could not define what those normal are anyway).

For example, if you want to do the same with a parabola instead, just change f

import numpy as np
import matplotlib.pyplot as plt

r = 2
h = 0
k = 0

x0 = h-r
x1 = h r


def f(x):
    return x**2

dx=0.001
x = np.linspace(x0 dx,x1-dx,9)
y = f(x)
def fprime(x):
    return (f(x dx)-f(x-dx))/(2*dx)

plt.scatter(x,y)
plt.quiver(x,f(x), -fprime(x)/np.sqrt(fprime(x)**2 1), 1/np.sqrt(fprime(x)**2 1))

plt.xlim(-4,4)
plt.ylim(-2,5)
plt.show()

All I changed here is the f formula. Not need for a new reasoning to compute the normal.

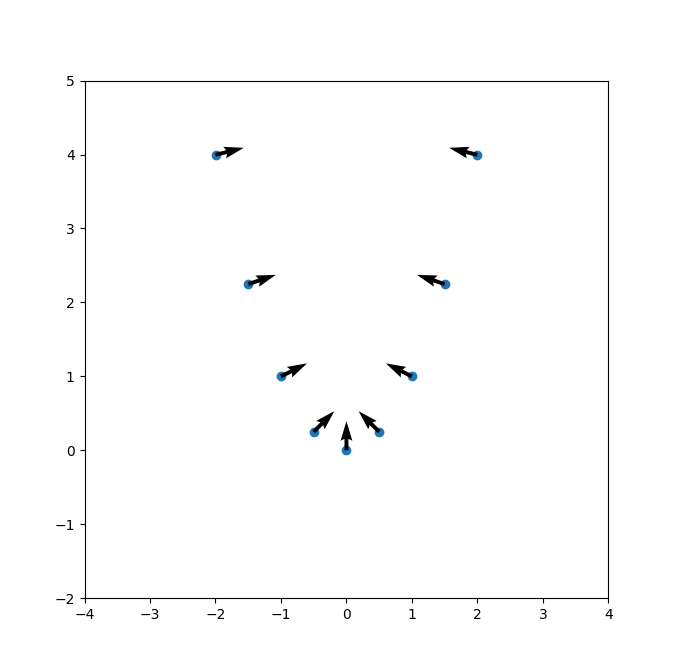
Last remark: an even more accurate version (not forcing the approximate computation of fprime with a dx) would be to use sympy to define f, and then compute the real, symbolic, derivative of f. But that doesn't seem necessary for your case.