I have been working on this to plot a function and rotating toward y and x axis. Then use SymPy to obtain the surface area.

I try from terminal and from running the .py file, both taking too long for calculating the integral to obtain the surface area.

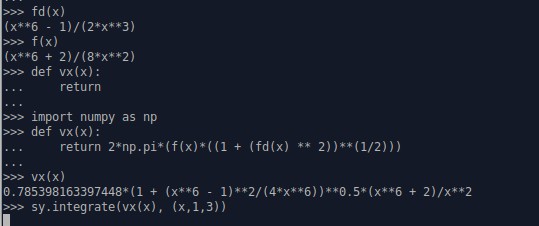
this is my code:

import numpy as np
import sympy as sy

x = sy.Symbol("x")

def f(x):
    return ((x**6)   2)/ (8*x ** 2)

def fd(x):
    return sy.simplify(sy.diff(f(x), x))

def vx(x):
    return 2*np.pi*(f(x)*((1   (fd(x) ** 2))**(1/2)))

vx = sy.integrate(vx(x), (x, 1, 3))

My questions:

1. Why sy.integrate took so long? almost 30 minutes.. is this function hard to be computed?

From terminal it has not even finished to calculate the integral till the time I ask this question at SoF:

2. Are there errors in my code or way of improvements for my code?

3. [Edited]

This is the answer from the sy.integrate:

0.392699081698724*Integral(2*(x**2   1)**1.0*Abs(x**4 - x**2   1)**1.0/x**5.0, (x, 1, 3))   0.392699081698724*Integral(x**1.0*(x**2   1)**1.0*Abs(x**4 - x**2   1)**1.0, (x, 1, 3))

why it does not substitute the x values into the definite integral?

Is

sy.integrate(vx(x), (x, 1, 3))

wrong to calculate a definite integral?

CodePudding user response：

I can't reproduce the behaviour that you see. Possible differences are the SymPy version (are you using the latest version?) and also whether or not gmpy2 is installed. Installing gmpy2 can speed up some operations in SymPy a lot.

Also you seem to be mixing floats and numpy things together. You need to decide if you want an exact result or not. If you want an exact result then use sympy's pi rather than the numpy one and also use exact rational numbers rather than the float 1/2. Along with a call to simplify before integrating this will give the exact result:

In [20]: import numpy as np
    ...: import sympy as sy
    ...: 
    ...: x = sy.Symbol("x")
    ...: 
    ...: def f(x):
    ...:     return ((x**6)   2)/ (8*x ** 2)
    ...: 
    ...: def fd(x):
    ...:     return sy.simplify(sy.diff(f(x), x))
    ...: 
    ...: def vx(x):
    ...:     return 2*sy.pi*(f(x)*sy.sqrt(1   (fd(x) ** 2)))
    ...: 
    ...: vxi = sy.Integral(vx(x), (x, 1, 3))

In [21]: %time vxi.simplify().doit()
CPU times: user 1.74 s, sys: 0 ns, total: 1.74 s
Wall time: 1.74 s
Out[21]: 
8429⋅π
──────
  81  

In [22]: _.evalf()
Out[22]: 326.919561445782

The fact that you are using floats suggests that you are not interested in an exact result in which case it is better to just evaluate the integral numerically:

In [23]: %time vxi.evalf()
CPU times: user 392 ms, sys: 0 ns, total: 392 ms
Wall time: 388 ms
Out[23]: 326.919561445782