Find at what point you will reach image border while walking from a certain point at a certain angle-CodePudding

I am doing some image processing and let us say that I have a point (e.g. (1000, 1000)) and an angle (e.g. 30 degrees), and I need to figure out at what point will I touch the border of the image (0, y) or (0, x) if I walked from that point at given angle. I can do it iteratively by just doing through an iterator and walking one step at a time, by doing in this example:

for i in range:
    x = 1000 - i * cos(30)
    y = 1000 - i * sin(30)

but maybe there is a better way to straight up find at which point will I hit the image border? I added image for clarity.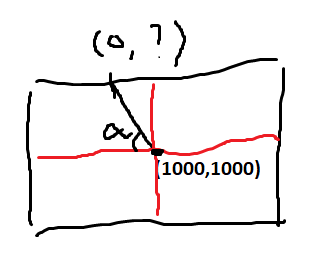

CodePudding user response：

Let's call (x0, y0) = (1000, 1000) your starting point.

Assuming you already know that the intersection point will be on the upper side of the box, then you are looking for a point (x, 0) such that cotan(alpha) = (x - x0) * y0.

So you can just choose x = x0 cotan(alpha) / y0.

Trigonometry function cotan isn't directly part of python's standard library, but cotan(alpha) = tan(pi/2 - alpha), so you can write:

import math

x = x0   math.tan(math.pi / 2 - alpha) / y0  # angle alpha in radians

Or alternatively:

import math

x = x0   math.tan((90 - alpha_in_degrees) * math.pi / 180) / y0

If your box is defined by coordinates (left, right, top, bottom) = (0, ?, 0, ?), then you can check that the point was indeed on the top side of the box by checking that the calculated value for x is in range, and that alpha is between 0 and 180°:

assert(left <= x <= right and 0 <= alpha_in_degrees <= 180)

CodePudding user response：

Time for some trigonometry, consider triangle like below

 
|\
| \
|  \
|   \
|   a\
 -----

its height is known to be 1000, its width is unknown, so denote it by x and value of angle a is known. tan function value is defined as ratio between opposite and adjacent in this case tan(a) = 1000/x which is equivalent to tan(a)*x = 1000 which is equivalent to x = 1000/tan(a).

After finding x rememeber you needs to subtract it from 1000, as your computing position in relation to (1000,1000)