given an array nums of integers with length n, for each index i, I am trying to find the rightmost index j such that i < j and nums[j] >= nums[i]. Is there an O(N) solution for this problem? I am aware of monotonic stack which could be used for this kind of problems, but unable to derive an algorithm.

For example, given an array A: A = [9,8,1,0,1,9,4,0,4,1], the solution should output [5,5,9,9,9,-1,8,9,-1,-1]. Here -1 indicates no indices satisfy the constraint.

This link asked the same question, and the accepted answer is only for O(NlogN). I'd like to know whether an O(N) solution is possible.

Thank you.

Update

Based on @Aivean's answer, here is an O(Nlog(N)) solution in python.

def rightmostGreaterOrEqual(nums):
    A, n = nums, len(nums)    
    indx = [-1]*n 
    stack, stackv = [], []
    for i in range(n-1, -1, -1):
        if not stack or nums[stack[-1]] < nums[i]:
            stack.append(i) 
            stackv.append(nums[i])
        else:
            idx = bisect.bisect_left(stackv, nums[i])
            indx[i] = stack[idx]
    return indx

B = [9,8,1,0,1,9,4,0,4,1]
rightGreat = rightmostGreaterOrEqual(B)
print(B)
[9, 8, 1, 0, 1, 9, 4, 0, 4, 1]
print(rightGreat)
[5, 5, 9, 9, 9, -1, 8, 9, -1, -1]

CodePudding user response：

There is not going to be an O(N) algorithm for the problem as written. Given a function that solves this problem, you could use it to partition N/2 arbitrary numbers into N/2 arbitrary adjacent ranges.

For example [2532,1463,3264,200,4000,3000,2000,1000] produces [5,6,4,7,-1,-1,-1,-1], identifying the ranges of the first N/2 numbers.

If you can only relate the numbers by comparison, then this will take you N/2 * log(N/2) comparisons, so O(N log N) time.

Without a limit on the size of the numbers, which would let you cheat like a radix sort, there isn't going to be way that is asymptotically faster than all comparison-based methods.

CodePudding user response：

The two problems of finding leftmost and rightmost j for a given i are not symmetrical, because of the added constraint of i < j. When I'm talking about these two tasks I assume that the constraint i < j is not flipped. This constraint means, that we always look to the right of i when searching for j, whether we're looking for rightmost or leftmost j. Without this constraint two tasks would be symmetrical.

1. Finding rightmost j, such that i < j and nums[i] ≤ nums[j]

One way to solve this task, is to traverse nums from right to left and maintain the strictly increasing subsequence of already visited elements (with their indices). Current element is added to the sequence only if it's larger, than the largest element already present in the sequence. Adding new element into the sequence is O(1).

For each element of nums you have to perform binary search in the subsequence of the visited elements to find the value that is larger or equals than the current element. Binary search is O(log n).

The total time is O(n log n), the auxiliary space needed is O(n).

Here is the graphical representation of the problem:

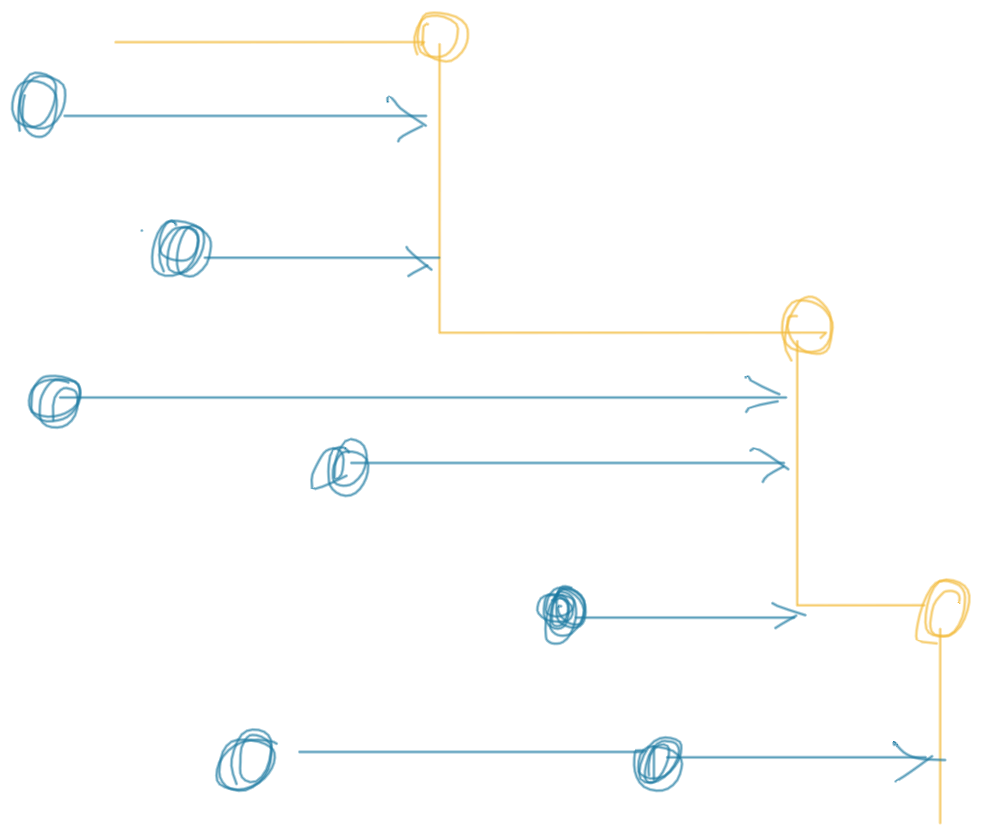
Here yellow dots represent the elements that form strictly increasing sequence (and their answer will be -1). Every other element (in blue) picks one of the ranges formed by yellow elements.

2. Finding leftmost j, such that i < j and nums[i] ≤ nums[j]

This problem, as opposed to the previous one, can be solved in O(n) time and O(n) space using monotonic stack. Similar to the previous problem, as you traverse nums from right to left, you form and maintain a monotonic stack, but, importantly, when new element is added to the stack all elements that are smaller are removed from the stack. And instead of using binary search to find the larger element, the answer is right at the new top of the stack (after all smaller elements were removed). This makes updating the stack and finding the answer for each element amortized O(1).

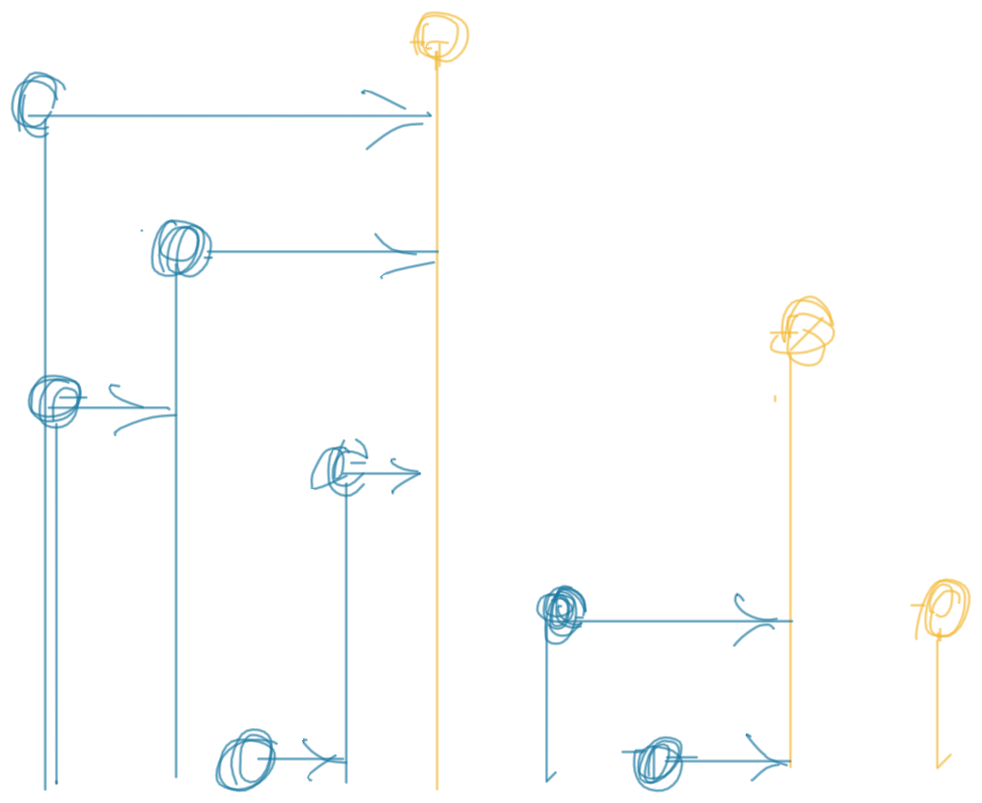
Here yellow elements represent elements with answer = -1, when they were added to the stack, they emptied the stack completely, as they were larger than every other element in the stack.