This has happened to me several times with different equations, and right now, I struggle with it again. I am sure others have the same problem and look for a memorable strategy to shape arrays and vectors so that non-trivial NumPy computations go through without fiddling and poking.
This is the equation I want to implement: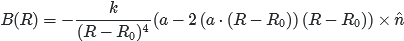 
, where k is a scalar, and n, a, R and R0 are 3D vectors. R0 is a NumPy array holding four 3D vectors.
Now I get stuck in my workflow because I try to find a way to pierce together the NumPy calculation. I want to use NumPy's awesome parallelization for math and not break up the four 3D vectors and do a for-loop. I am not good enough at NumPy to "see" the shapes of intermediate result arrays. And so I end up with try-and-error, which gives ugly results and is unsatisfying.
Please don't just give a working solution but explain why you did what you did.
Here is my current code - which does not work as it should (the transposing of random arrays should not be there).
import numpy as np
def main():
r_0 = np.array([[.265, 0, .382],
[0, .712, .764],
[0, .712, 0],
[.752, .712, .382]])
b_measured = np.array([[1.64712096, 4.87716371, -0.77060129],
[1.55980676, 4.93977942, -0.7133636],
[1.40883668, 4.96624651, -0.71742247],
[1.6531721, 5.02004066, -0.72243437]])
n = np.array([0, 0, 1])
a = np.array([.2, 0, 0])
r = np.array([0, 2, 0])
r_relativ = (r - r_0)
r_magnitude = np.linalg.norm(r_relativ, axis=1)
error = -np.cross(a - 2 * (r_relativ.T * np.matmul(r_relativ, a)).T, n,
axisa=1) / r_magnitude ** 4 - b_measured
print(error)
if '__name__' == '__main__':
main()
CodePudding user response：
This is a casting problem from numpy. In this line:
r_magnitude = np.linalg.norm(r_relativ, axis=1)
you are getting a (4,) shape, which is a vector, not an array. You can check that by adding a
print(r_magnitude.shape)
This generates difficulties with numpy casting, as numpy doesn't quite know how to cast this second undefined dimension. That is why you probably get the error
ValueError: operands could not be broadcast together with shapes (4,3) (4,)
Which means, you are trying to broadcast your vector r_magnitude (shape = (4,)) into a (4,3) shaped numpy array. To understand why this happens, you can check this link to Tutorialspoint. Towards the end they explain it.
What I believe is the standard, is to use the keepdims kwarg for basically every numpy method.
r_magnitude = np.linalg.norm(r_relativ, axis=1, keepdims=True)
This will make the operation keep the same number of dimentions as the original array (2 in this case), that is, r_magnitude's shape is now (4,1), making the broadcasting possible
CodePudding user response：
Keeping track of shapes is a large part of numpy coding (and before that MATLAB).
First, I like to have a clear idea of the shapes of the inputs:
In [1]: r_0 = np.array([[.265, 0, .382],
...: [0, .712, .764],
...: [0, .712, 0],
...: [.752, .712, .382]])
...:
...: b_measured = np.array([[1.64712096, 4.87716371, -0.77060129],
...: [1.55980676, 4.93977942, -0.7133636],
...: [1.40883668, 4.96624651, -0.71742247],
...: [1.6531721, 5.02004066, -0.72243437]])
...:
...: n = np.array([0, 0, 1])
...: a = np.array([.2, 0, 0])
...: r = np.array([0, 2, 0])
...:
In [2]: r_0.shape
Out[2]: (4, 3)
In [3]: b_measured.shape
Out[3]: (4, 3)
The rest are (3,)
While one can use the debugger, I prefer to test code in an interactive session like ipython.
In [4]: r_relativ = (r - r_0) # this was a (4,3) broadcasting with (3,)
In [5]: r_relativ.shape
Out[5]: (4, 3)
norm with axis, is like sum, mean etc, a reduction function, removing a dimension:
In [6]: r_magnitude = np.linalg.norm(r_relativ, axis=1)
In [7]: r_magnitude.shape
Out[7]: (4,)
though it is possible retain that dimension as a broadcastable size 1:
In [8]: np.linalg.norm(r_relativ, axis=1, keepdims=True).shape
Out[8]: (4, 1)
Your next line is complex, and the error doesn't identify the operator:
In [9]: error = -np.cross(a - 2 * (r_relativ.T * np.matmul(r_relativ, a)).T, n,
...: axisa=1) / r_magnitude ** 4 - b_measured
Traceback (most recent call last):
File "<ipython-input-9-8d7646046c43>", line 1, in <module>
error = -np.cross(a - 2 * (r_relativ.T * np.matmul(r_relativ, a)).T, n,
ValueError: operands could not be broadcast together with shapes (4,3) (4,)
Looking at the individual pieces:
In [10]: np.matmul(r_relativ, a).shape
Out[10]: (4,)
This is a (4,3) with (3,) producing a (4,). (Also matmul issues different error messages).
In [11]: (r_relativ.T * np.matmul(r_relativ, a)).T.shape
Out[11]: (4, 3)
The cross argument looks ok. cross itself runs. I don't use it enough to remember the exact axis arguments, though the basic operation is for a pair of (N,3) arrays
In [13]: np.cross(a - 2 * (r_relativ.T * np.matmul(r_relativ, a)).T, n,
...: axisa=1).shape
Out[13]: (4, 3)
Finally, here's the error:
In [15]: np.cross(a - 2 * (r_relativ.T * np.matmul(r_relativ, a)).T, n,
...: axisa=1)/r_magnitude**4
Traceback (most recent call last):
File "<ipython-input-15-c4bed1fd9807>", line 1, in <module>
np.cross(a - 2 * (r_relativ.T * np.matmul(r_relativ, a)).T, n,
ValueError: operands could not be broadcast together with shapes (4,3) (4,)
Why? As noted the cross produces (4,3). But r_magnitude is (4,). It should be (4,1) to work with the (4,3).
In sum, I keep the 2 broadcasting rules upper most - it can add leading dimensions, and size 1 dimensions can be scaled to match.
The other issue is keeping track of how reductions like norm change the dimensions. keepdims can be a big help here, though it's always possible to use None to add trailing dimensions.
I don't think there's any short cut to being pedantic about the dimensions. Details matter.
With the (4,) correction to (4,1), error runs:
In [16]: r_magnitude = np.linalg.norm(r_relativ, axis=1, keepdims=True)
In [17]: error = -np.cross(a - 2 * (r_relativ.T * np.matmul(r_relativ, a)).T, n,
...:
...: axisa=1) / r_magnitude ** 4 - b_measured
In [18]: error.shape
Out[18]: (4, 3)