Find coordinates of points given their distances-CodePudding

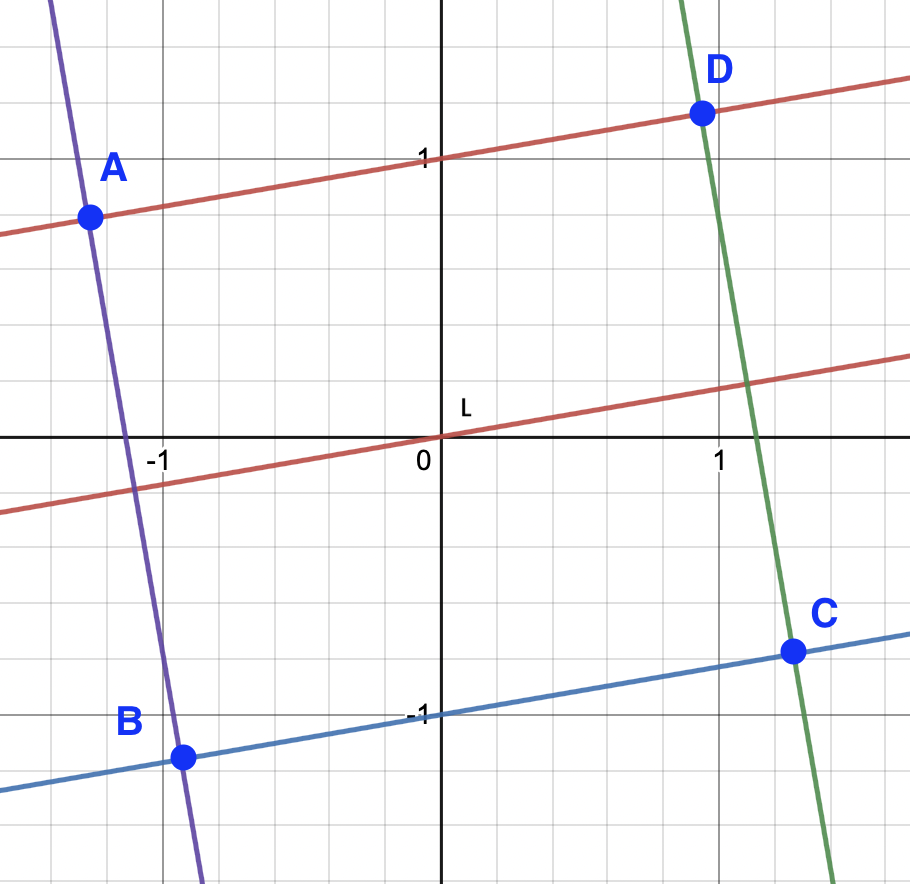
I have to find in Python the coordinates of the points A, B, C, D given their distances and the gradient of the line L (the one that passes through the center), which is parallel to segments AD and BC and orthogonal to segments AB and CD.

That is the code I wrote:

import numpy as np

# Gradient of the known line
l_gradient = 0.17
l_angle = np.arctan(l_gradient)

# Length of the segments
ad_distance =  1
ab_distance =  2

# Gradient and Intercept of lines AB and DC with the y axes 
ab_gradient = dc_gradient = -1 / l_gradient # orthogonal to L
dc_intercept = (ad_distance / 2) / np.sin(l_angle) # Inverse formula of the right triangle
ab_intercept = - dc_intercept

# Gradient and Intercept of lines AD and BC with the y axes 
ad_gradient = bc_gradient = l_gradient # parallel to L
ad_intercept = (ab_distance / 2) / np.cos(l_angle) # Inverse formula of the right triangle
bc_intercept = - ad_intercept

CodePudding user response：

I think the easiest way to do this is first assume the gradient is 0. Then we have our points:

ad_distance = 1
ab_distance = 2
points = np.array([
    [-ad_distance / 2,  ab_distance / 2],  # A
    [-ad_distance / 2, -ab_distance / 2],  # B
    [ ad_distance / 2, -ab_distance / 2],  # C
    [ ad_distance / 2,  ab_distance / 2],  # D
])

Note that at the bottom we have a triangle with sides (x, l_gradient x, sqrt(1 l_gradient^2) x). And remember cos(angle) = adjacent / hypot.

Thus we have:

l_gradient = 0.17
l_cos = 1 / np.sqrt(1   l_gradient**2)
l_sin = l_gradient * l_cos

Now we can use those to construct a rotation matrix, and rotate our points into the correct positions:

l_rot = np.array([[l_cos , -l_sin], [l_sin, l_cos]])
points = (l_rot @ points.T).T

No trigonometry functions required!