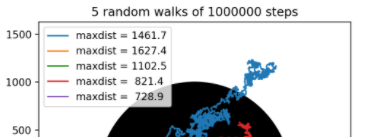
Find max distance from (0,0) and add to legend matplotlib-CodePudding

I have this code calculating a random walk that I am trying to find the max distance from (0.0) for all walks and add them to a legend. Added an image of the result I want to achieve.

import numpy as np
import matplotlib.pyplot as plt
import math

np.random.seed(12)
repeats = 5 
N_steps = 1000000
expected_R = np.sqrt(N_steps)

plt.title(f"{repeats} random walks of {N_steps} steps")

for x in range(repeats):
    dirs = np.random.randint(0, 4, N_steps)
    steps = np.empty((N_steps, 2))

    steps[dirs == 0] = [0, 1]  # 0 - right
    steps[dirs == 1] = [0, -1]  # 1 - left
    steps[dirs == 2] = [1, 0]  # 2 - up
    steps[dirs == 3] = [-1, 0]  # 3 - down
        
    steps = steps.cumsum(axis=0)

    print("Final position:", steps[-1])

    skip = N_steps // 5000   1
    xs = steps[::skip, 0]
    ys = steps[::skip, 1]

    x = max(ys)

    plt.plot(xs, ys)
    

circle = plt.Circle((0, 0), radius=expected_R, color="k")
plt.gcf().gca().add_artist(circle)
plt.gcf().gca().set_aspect("equal")
plt.axis([-1500-x,1500 x,-1500-x,1500 x])

plt.show()

CodePudding user response：

You can plot the distance from the coordinates steps to 0,0 by using distance=np.linalg.norm(steps, axis=1). And you can then take the max of this array to find the maximum distance. You can then add a label to your plots and a legend. See code below:

import numpy as np
import matplotlib.pyplot as plt
import math

np.random.seed(12)
repeats = 5 
N_steps = 1000000
expected_R = np.sqrt(N_steps)

plt.title(f"{repeats} random walks of {N_steps} steps")
max_distance=np.zeros(repeats)
for x in range(repeats):
    dirs = np.random.randint(0, 4, N_steps)
    steps = np.empty((N_steps, 2))

    steps[dirs == 0] = [0, 1]  # 0 - right
    steps[dirs == 1] = [0, -1]  # 1 - left
    steps[dirs == 2] = [1, 0]  # 2 - up
    steps[dirs == 3] = [-1, 0]  # 3 - down
        
    steps = steps.cumsum(axis=0)

    print("Final position:", steps[-1])

    skip = N_steps // 5000   1
    xs = steps[::skip, 0]
    ys = steps[::skip, 1]
    distance=np.linalg.norm(steps, axis=1)
    max_distance[x]=np.amax(distance)
    plt.plot(xs, ys,label='Random walk ' str(x) ': max distance: ' str(np.round(max_distance[x],1)))
    

circle = plt.Circle((0, 0), radius=expected_R, color="k")
plt.gcf().gca().add_artist(circle)
plt.gcf().gca().set_aspect("equal")
plt.axis([-1500-x,1500 x,-1500-x,1500 x])
plt.legend(fontsize=8)
plt.show()

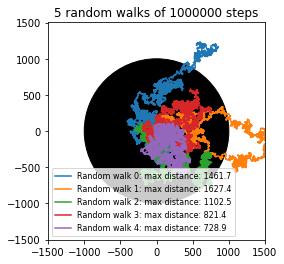
And the output gives: