Cannot seem to resolve ambiguity in Antlr Grammar-CodePudding

I am creating the simplest grammar possible that basically recognizes arithmetic expressions. The grammar needs to correctly follow arithmetic operators precedence rules (PEMDAS), and for that I placed expr ('*'|'/') term before expr (' '|'-') term to ensure this precedence. This is the arithmetic.g4 file that I have:


/*Productions */
 
expr: expr ('*'|'/') term
    | expr (' '|'-') term
    | term
    ;
term: '('expr')'
    | ID
    | NUM
    ;

/*Tokens */
ID: [a-z] ;
NUM: [0-9] ;

WS:  [\t\r\n] ->skip;

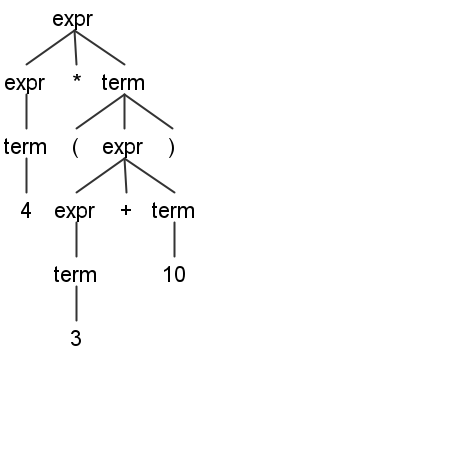
The output of the grammar is however not what it should be. For example for the arithmetic expression 4 * (3 10) I get the below parse tree (which is absolutely not correct):

Any suggestions on how I can change the grammar to get what I am looking for. I am new to antlr and am not sure what mistake I am making. (jbtw my OS is windows)

CodePudding user response：

(I'm assuming that you've made a mistake in your example (which looks fine) and you really meant that you're getting the wrong tree for the input 4 3 * 10, so that's what I'm going to answer. If that's not what you meant, please clarify.)

You're right that ANTLR resolves ambiguities based on the order of rules, but that does not apply to your grammar because your grammar is not ambiguous. For an input like 4 3 * 10, there's only one way to parse it according to your grammar: with * being the outer operator, with 4 3 as its left and 10 as its right operand. The correct way ( as the outer operator with 3 * 10 as the right operand) doesn't work with your grammar because 3 * 10 is not a valid term and the right operand needs to be a term according to your grammar.

In order to get an ambiguity that's resolved in the way you want, you'll need to make both operands of your operators exprs.