fast matching in arrays for double auction-CodePudding

I'm implementing a matching system for a double auction. I have buy and sell arrays of orders, with [price, quantity] for each order. For example, buy:

[[ 2 44]
 [ 6 47]
 [10 64]
 [ 4 67]
 [ 1 67]
 [ 6  9]
 [ 1 83]
 [ 2 21]
 [ 3 36]
 [ 5 87]
 [ 3 70]]

So the first buy order was for 44 units with price 2. Prices are limited to a price grid e.g. 1, 2, ..., 10. For each possible price I create cumulative arrays showing aggregate demand and supply. For example for aggregate demand I look at cumulative quantity for each price P on the price grid, summing for all buy orders with price greater or equal than P. Then I find the clearing price being the price such that aggregate buy orders are smaller than aggregate sell orders. The clearing quantity is the smaller of the aggregate levels at the cleared price.

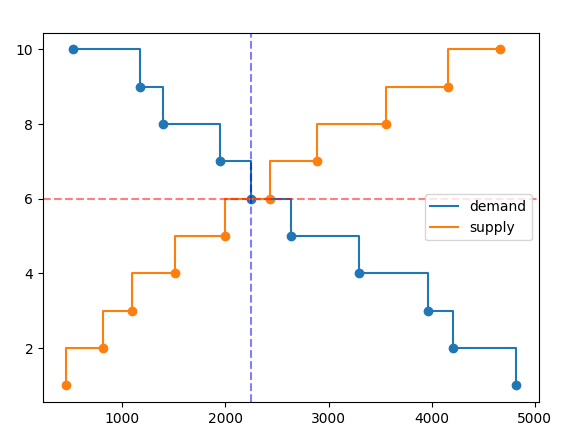
For example here the cleared price is 6 (red dashed) and the cleared quantity around 2250 (blue dashed)

My question, is there a faster/cleaner way to compute the cleared price? How can I make it more efficient, assuming the price grid becomes very fine (eg.10000 possible prices), without having to check for each possible price level? Speed and efficiency are the main issues.

Showing here implementation in Python (production will likely be in other lower-level language)

import numpy as np

MAX_QTY = 100
MIN_QTY = 0
MIN_PX = 1
MAX_PX = 11
TICK_SIZE = 1

price_grid = np.arange(MIN_PX, MAX_PX, TICK_SIZE)

def gen_orders(num, price_grid):
    qty = np.random.randint(MIN_QTY, MAX_QTY, num)
    px = np.random.choice(price_grid, num)
    return np.array((px, qty)).T

buy = gen_orders(100, price_grid)
sell = gen_orders(100, price_grid)

agg = np.array([[x, np.sum(buy[buy[:, 0]>=x][:, 1]), np.sum(sell[sell[:, 0]<=x][:, 1])] for x in price_grid])

matched = agg[agg[:, 1]<agg[:, 2]][0, :] # price_grid is sorted
cleared_px = matched[0]
cleared_qty = np.min(matched[1:])

CodePudding user response：

There are a few tricks you could try:

Stopping when the quantity matched, as shown in this notebook

buy_sum = np.sum(buy[buy[:, 0]>=x][:, 1])
sell_sum = np.sum(sell[sell[:, 0]<=x][:, 1])

if buy_sum < sell_sum:
    cleared_px = x
    cleared_qty = buy_sum
    break

Sort the buy and sell orders first such that the sum_of_quantity function can be faster when you loop through buy and sell. Unfortunately, there are a lot of overhead with for loop in Python, so it's simply faster to just use numpy vectorized operations like np.sum(buy[buy[:, 0]>=x][:, 1]) in Python. However, this will be useful in lower-level language.
Cache the sum values, say in bins, if you have sorted the buy and sell orders. For example, you can store the sum of x <= 4 in memory, so when you want to calculate sum of x <= 5, you can use sum of x <= 4 plus the sum of x == 5. This requires keeping track of the indexes where x changes, in the order list. Note that it cannot be used with numpy vectorized operations, because doing buy[:, 0]==5 is just as expensive as buy[:, 0]<=5 with numpy.
Try approaches like search algorithms. This will be useful for larger search space, i.e. price_grid has much more values. For example with price_grid <= 10,
- Try with x == 5 first.
- If it turns out buy_sum > sell_sum, try some x that is larger, e.g. x == 7.
- If buy_sum < sell_sum, confirm it's the best price by check x is x - 1; otherwise, pick a even smaller x that is larger than 5 and repeat

CodePudding user response：

You are implicitly creating a couple of nested loops in this statement:

agg = np.array([[x, np.sum(buy[buy[:, 0]>=x][:, 1]), np.sum(sell[sell[:, 0]<=x][:, 1])] for x in price_grid])

Even though they are executed largely in vectorized format, that is eating you up when the price grid is huge or the order qty is huge.

You can do this in linear fashion by binning the orders. I use a dictionary below. Then, one more linear pass through the buys dictionary to create the aggregate demand number you need, which is all still O(n) instead of O(n^2).

For larger n, this is a huge change. I timed the orig and mod (below) and for 5000 orders and a 10K price grid (your value), this mod is 100x faster without numpy operations at all.

Note: there is a slight logic difference in that the mod stops early if supply == demand exactly at any price step. (Not clear if this is a bug or feature... :), but the logic could be tweaked easy enough). I've shown a capture of the (somewhat rare) occurrence that they match with time differences.

Edited Code w/ timing

import numpy as np
import time

MAX_QTY = 10
MIN_QTY = 0
MIN_PX = 1
MAX_PX = 10_000
TICK_SIZE = 1

price_grid = np.arange(MIN_PX, MAX_PX, TICK_SIZE)

def gen_orders(num, price_grid):
    qty = np.random.randint(MIN_QTY, MAX_QTY, num)
    px = np.random.choice(price_grid, num)
    return np.array((px, qty)).T

buy = gen_orders(5000, price_grid)
sell = gen_orders(5000, price_grid)

tic = time.time() 
agg = np.array([[x, np.sum(buy[buy[:, 0]>=x][:, 1]), np.sum(sell[sell[:, 0]<=x][:, 1])] for x in price_grid])
matched = agg[agg[:, 1]<agg[:, 2]][0, :] # price_grid is sorted
cleared_px = matched[0]
cleared_qty = np.min(matched[1:])
toc = time.time()
print(f'ORIG: computed clear px: {cleared_px} and qty: {cleared_qty} in {toc-tic:0.6f} sec')

###  ALTERNATE ###

# Start the clock again for the mod method...
tic = time.time()
buys = {}
sells = {}
# "bin" the buys by price
for b in buy:
    buys[b[0]] = buys.get(b[0], 0)   b[1]
# need to aggregate the demand...
agg_demand = {MAX_PX: buys.get(MAX_PX,0)} # starting point
for px in range(MAX_PX-1, MIN_PX-1, -1):  # backfill down to min px
    agg_demand[px] = agg_demand[px 1]   buys.get(px, 0)

# "bin" the sells similarly
for s in sell:
    sells[s[0]] = sells.get(s[0], 0)   s[1]

# set up the loop
selling_px = MIN_PX
supply = sells.get(selling_px, 0)
demand = agg_demand.get(selling_px, 0)
while demand > supply:
    # updates
    selling_px  = 1
    demand = agg_demand.get(selling_px) # update with the pre-computed aggregate demand
    supply  = sells.get(selling_px, 0)  # keep running aggregation of supply
new_cleared_px = selling_px
new_cleared_qty = min(demand, supply)


toc = time.time()
print(f'MOD: computed clear px: {new_cleared_px} and qty: {new_cleared_qty} in {toc-tic:0.6f} sec')

if cleared_px != new_cleared_px or cleared_qty != new_cleared_qty:  # somethign wrong...??
    print(agg[cleared_px-5:cleared_px 5,:])

Output:

ORIG: computed clear px: 4902 and qty: 11390 in 1.183204 sec
MOD: computed clear px: 4899 and qty: 11398 in 0.020830 sec
[[ 4898 11411 11398]
 [ 4899 11398 11398]
 [ 4900 11398 11398]
 [ 4901 11398 11398]
 [ 4902 11390 11398]
 [ 4903 11385 11398]
 [ 4904 11385 11398]
 [ 4905 11385 11398]
 [ 4906 11385 11398]
 [ 4907 11384 11398]]
[Finished in 1.3s]