NumPy: balancing water levels between bins of different depths-CodePudding

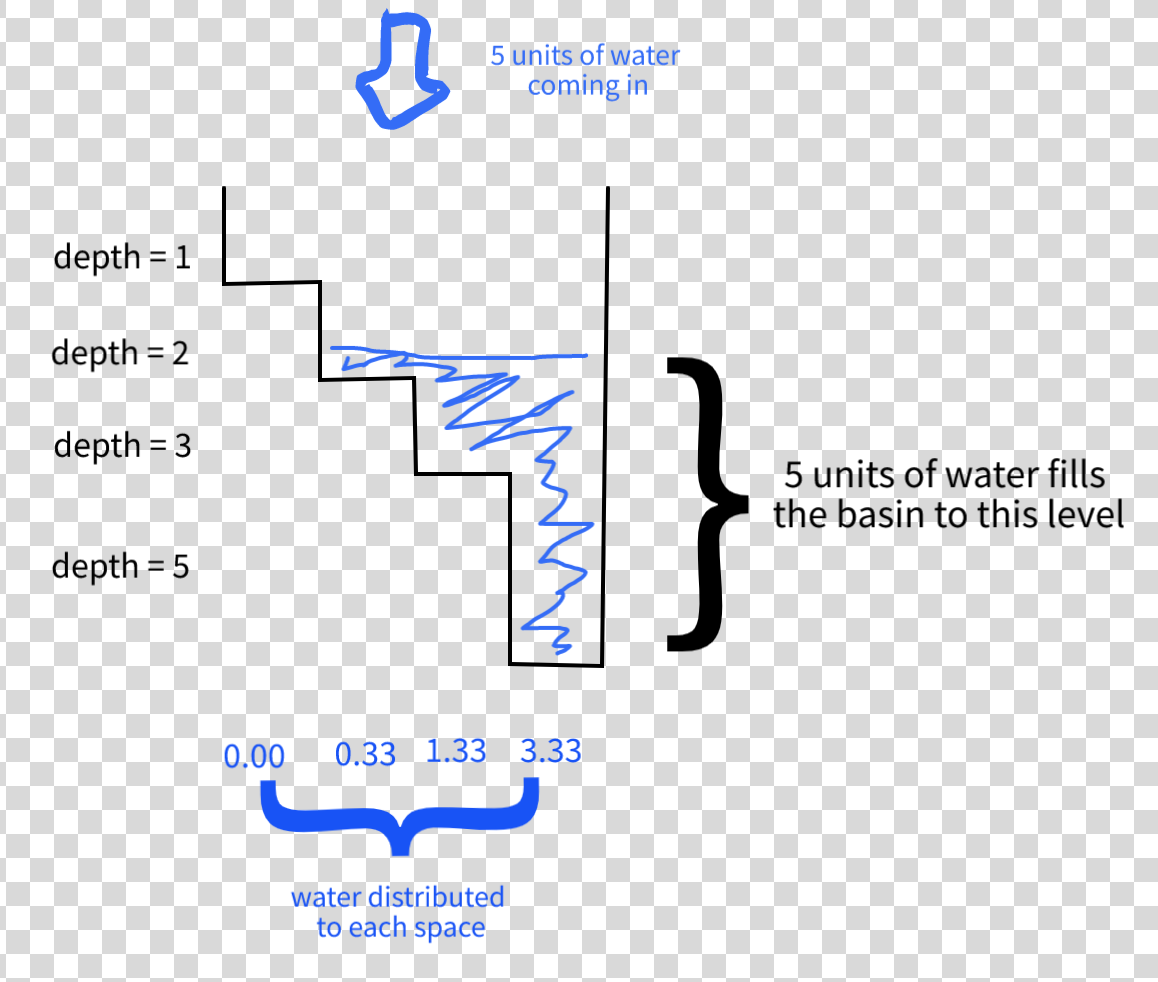
I am implementing a simulation in NumPy, and as part of the update step for the simulation, I need to solve the following problem. There is some water that is going to be distributed among a set of connected bins of different depths. I need to find the amount of water to put in each bin such that the overall water level is the same.

So, for example, if there are 4 bins with depths 1, 2, 3 and 5, and I have to distribute 5 units of water, I will distribute 3 1/3 units to the depth 5 bin, 1 1/3 units to the depth 3 bin, and 1/3 units to the depth 2 bin.

So, given an array of bin depths and an amount of water to distribute, I need to calculate an array that describes how much water to allocate into each bin.

I need a very high-performant solution because this particular routine gets called many many times during the simulation. Calculating this function might be the slowest part of the program. So, I kind of need a NumPy solution, avoiding Python if possible for performance reasons.

Edit: in the real problem, there are always less than 9 bins, but the exact number can vary. I can constrain the depth of the bins if that would help.

Anyone have any ideas?

CodePudding user response：

I got numpy implementation working. It could be optimized using numba though.

For others answering: There is one inconvenience - when some bins have same depth, the code needs to address that.

import numpy as np


def find_levels_numpy(bins, n_units):
    depth_diff = np.diff(bins)
    bin_bottom_level = np.concatenate([[0], np.cumsum(-depth_diff)])
    volume_for_bottom_bin = np.cumsum(np.concatenate([[0], -depth_diff]) * np.arange(len(bins)))
    # NOTE: results of the code above could be cached for given bins and reused for different n_units!

    idx_of_last_filled_bin = np.searchsorted(volume_for_bottom_bin, n_units) - 1
    levels = bin_bottom_level[idx_of_last_filled_bin] - bin_bottom_level
    remainder = n_units - volume_for_bottom_bin[idx_of_last_filled_bin]
    levels  = remainder / (idx_of_last_filled_bin   1)
    levels[idx_of_last_filled_bin 1:] = 0
    return levels


if __name__ == '__main__':
    # sorting bins for convenience
    bins = np.array([0.5, 5, 3, 2, 1, 1])
    n_units = 11
    sort_indices = np.argsort(bins)[::-1]
    bins = bins[sort_indices]
    level_by_bin = find_levels_numpy(bins, n_units)

    # undoing sorting
    level_by_bin[sort_indices] = level_by_bin[np.arange(len(sort_indices))]
    print(level_by_bin)
    print(np.sum(level_by_bin))

[0.25 4.75 2.75 1.75 0.75 0.75]
11.0