I try to measure the width of the individual grains of gravel. I need this to recognize whether it is fine gravel or coarse gravel. Could you help me, how can I find the 2 extreme parts of the gravel contour? Up to this point I was trying to get only the contours from the picture. (Photos under code) My current code:
import cv2
import numpy as np
def empty(a):
pass
path = "materials/gr2.jpeg"
path2 = "materials/gr1.jpeg"
cv2.namedWindow("TrackBars")
#cv2.resizeWindow("TrackBars",740,280)
cv2.createTrackbar("Hue Min", "TrackBars",0,179,empty)
cv2.createTrackbar("Hue Max", "TrackBars",179,179,empty)
cv2.createTrackbar("Sat Min", "TrackBars",0,255,empty)
cv2.createTrackbar("Sat Max", "TrackBars",255,255,empty)
cv2.createTrackbar("Val Min", "TrackBars",147,255,empty)
cv2.createTrackbar("Val Max", "TrackBars",255,255,empty)
img = cv2.imread(path)
img2 = cv2.imread(path2)
imgHSV = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)
imgHSV2 = cv2.cvtColor(img2, cv2.COLOR_BGR2HSV)
while True:
h_min = cv2.getTrackbarPos("Hue Min", "TrackBars")
h_max = cv2.getTrackbarPos("Hue Max", "TrackBars")
s_min = cv2.getTrackbarPos("Sat Min", "TrackBars")
s_max = cv2.getTrackbarPos("Sat Max", "TrackBars")
v_min = cv2.getTrackbarPos("Val Min", "TrackBars")
v_max = cv2.getTrackbarPos("Val Max", "TrackBars")
print(h_min,h_max,s_min,s_max,v_min,v_max)
lower = np.array([h_min,s_min,v_min])
upper = np.array([h_max,s_max,v_max])
mask = cv2.inRange(imgHSV,lower,upper)
mask2 = cv2.inRange(imgHSV2,lower,upper)
cv2.imshow("Mask2", mask2)
cv2.imshow("Mask", mask)
cv2.waitKey(1)
CodePudding user response:
Here are some statistics using laplacian pyramids.
Ignore the top few levels, which are due to uneven lighting and wet vs. dry gravel.
You can see in the lower/finer levels (towards 10) you get more response from the fine gravel, while the coarse gravel's response reaches higher up.
coarse vs fine
[ 0] 351399 : 385660 # ignore that, that's the DC component
[ 1] 75 : 95
[ 2] 177 : 184
[ 3] 130 : 78
[ 4] 408 : 94
[ 5] 1352 : 215
[ 6] 4051 : 706
[ 7] 7784 : 2123
[ 8] 8521 : 4814
[ 9] 6838 : 8108
[10] 8207 : 12775
#!/usr/bin/env python3
import os
import sys
from math import *
import numpy as np
import cv2 as cv
np.set_printoptions(suppress=True, linewidth=120)
im1 = cv.imread("coarse dCrrR.jpg", cv.IMREAD_GRAYSCALE)
im2 = cv.imread("fine xvmKD.jpg", cv.IMREAD_GRAYSCALE)
levels = 10
sw = sh = 2**levels
def take_sample(im):
h,w = im.shape[:2]
return im[(h-sh) // 2 : (h sh) // 2, (w-sw) // 2 : (w sw) // 2]
def gaussian_pyramid(sample):
gp = [sample]
for k in range(levels):
sample = cv.pyrDown(sample)
gp.append(sample)
return gp
def laplacian_pyramid(gp):
lp = [gp[-1]] # "base" gaussian
for k in reversed(range(levels)):
diff = gp[k] - cv.pyrUp(gp[k 1])
lp.append(diff)
return lp
sample1 = take_sample(im1) * np.float32(1/255)
sample2 = take_sample(im2) * np.float32(1/255)
gp1 = gaussian_pyramid(sample1)
gp2 = gaussian_pyramid(sample2)
lp1 = laplacian_pyramid(gp1)
lp2 = laplacian_pyramid(gp2)
print("coarse vs fine")
for i,(level1,level2) in enumerate(zip(lp1, lp2)):
area = 2**(2*i)
sse1 = (level1**2).sum() / area
sse2 = (level2**2).sum() / area
print(f"[{i:2d}] {sse1*1e6:8.0f} : {sse2*1e6:8.0f}")
CodePudding user response:
if a coarse estimation of the average gravel stone size in the image is enough, you could try this algorithm, which is really very coarse and maybe not accurate (you would have to test this for a lot more images whether it statistically makes sense)
1. threshold for bright gravel stones
2. subtract the edges between stones
3. extract external contours and discard too small ones (magic number)
4. choose any comparison point in the sorted contour area list (e.g. median = 50%)
Gives these results:
Fine image => median contour area: 31
Coarse image => median contour Area 89.5
with these mask images which are used to compute the contours:
From this source code:
int main()
{
try
{
cv::Mat img = cv::imread("C:/data/StackOverflow/gravel/coarse.jpg", cv::IMREAD_GRAYSCALE);
cv::Mat thresh;
double t = cv::threshold(img, thresh, 255, 255, cv::THRESH_OTSU | cv::THRESH_BINARY);
//thresh = img > t * 1.5; // doesnt work as well as removing the edges
cv::Mat sobelX, sobelY;
cv::Sobel(img, sobelX, CV_32FC1, 1, 0, 3, 1.0, 0);
cv::Sobel(img, sobelY, CV_32FC1, 0, 1, 3, 1.0, 0);
cv::Mat sobelMag_FC;
cv::Mat sobelMag_8U;
cv::Mat sobelBin;
cv::magnitude(sobelX, sobelY, sobelMag_FC);
sobelMag_FC.convertTo(sobelMag_8U, CV_8U);
double t2 = cv::threshold(sobelMag_8U, sobelBin, 255, 255, cv::THRESH_OTSU | cv::THRESH_BINARY);
//sobelBin = sobelMag_FC > 150; // doesnt work as well
cv::Mat gravel = thresh - sobelBin;
std::vector<std::vector<cv::Point> > contours;
cv::findContours(gravel, contours, cv::RETR_EXTERNAL, cv::CHAIN_APPROX_NONE);
std::vector<double> contourAreas;
for (int i = 0; i < contours.size(); i)
{
double area = cv::contourArea(contours[i]);
if(area > 10) contourAreas.push_back(area); // magic number for minimum contour area...
}
std::sort(contourAreas.begin(), contourAreas.end());
// choose a single comparison point (e.g. 50% position in the list => median)
std::cout << contourAreas.at(contourAreas.size() *0.5) << std::endl;
cv::imwrite("C:/data/StackOverflow/gravel/coarse_mask.png", gravel);
}
catch (std::exception& e)
{
std::cout << e.what() << std::endl;
std::cin.get();
}
}
You can see that there are maaaaany tiny contours and connected gravel stones etc. so probably the whole algorithm is garbage in the end, but gives some more or less reasonable relative size results for both images.
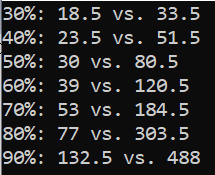
Adding a max-contour-size of 1000 and testing for more comparison points: