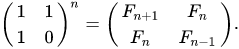I am trying to implement a code which works for retrieving Millionth Fibonacci number or beyond. I am using Matrix Multiplication with Numpy for faster calculations.
According to my understanding it should take O(logN) time and worst case for a million should result in: Nearly 6secs which should be alright.
Following is my implementation:
def fib(n):
import numpy as np
matrix = np.matrix([[1, 1], [1, 0]]) ** abs(n)
if n%2 == 0 and n < 0:
return -matrix[0,1]
return matrix[0, 1]
However, leave 1million, it is not even generating correct response for 1000
Actual response:
43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875
My Response:
817770325994397771
Why is Python truncating the responses generally from the docs it should be capable of calulating even 10**1000 values. Where did I go wrong?
CodePudding user response:
Numpy can handle numbers and calculations in a high-performance way (both memory efficiency and computing time). So while Python can process sufficiently large numbers, Numpy can't. You can let Python do the calculation and get the result, exchanging with performance reduction.
Sample code:
import numpy as np
def fib(n):
# the difference is dtype=object, it will let python do the calculation
matrix = np.matrix([[1, 1], [1, 0]], dtype=object) ** abs(n)
if n%2 == 0 and n < 0:
return -matrix[0,1]
return matrix[0, 1]
print(fib(1000))
Output:
43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875
PS: Warning
Milionth Fibonacci number is extremely large, you should make sure that Python can handle it. If not, you will have to implement/find some module to handle these large numbers.
CodePudding user response:
I'm not convinced that numpy is much help here as it does not directly support Python's very large integers in vectorized operations. A basic Python implementation of an O(logN) algorithm gets the 1 millionth Fibonacci number in 0.15 sec on my laptop. An iterative (slow) approach gets it in 12 seconds.:
def slowfibo(N):
a = 0
b = 1
for _ in range(1,N): a,b = b,a b
return a
# Nth Fibonacci number (exponential iterations) O(log(N)) time (N>=0)
def fastFibo(N):
a,b = 1,1
f0,f1 = 0,1
r,s = (1,1) if N&1 else (0,1)
N //=2
while N > 0:
a,b = f0*a f1*b, f0*b f1*(a b)
f0,f1 = b-a,a
if N&1: r,s = f0*r f1*s, f0*s f1*(r s)
N //= 2
return r
output:
f1K = slowFibo(1000) # 0.00009 sec
f1K = fib(1000) # 0.00011 sec (tandat's)
f1K = fastFibo(1000) # 0.00002 sec
43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875
f1M = slowFibo(1_000_000) # 12.52 sec
f1M = fib(1_000_000) # 0.2769 sec (tandat's)
f1M = fastFibo(1_000_000) # 0.14718 sec
19532821287077577316...68996526838242546875
len(str(f1M)) # 208988 digits
CodePudding user response:
The core of your function is
np.matrix([[1, 1], [1, 0]]) ** abs(n)
which is discussed in the Wiki article
np.matrix implements ** as __pwr__, which in turn uses np.linalg.matrix_power. Essentially that's a repeated dot matrix multiplication, with a modest enhancement by grouping the products by powers of 2.
In [319]: M=np.matrix([[1, 1], [1, 0]])
In [320]: M**10
Out[320]:
matrix([[89, 55],
[55, 34]])
The use of np.matrix is discouraged, so I can do the same with
In [321]: A = np.array(M)
In [322]: A
Out[322]:
array([[1, 1],
[1, 0]])
In [323]: np.linalg.matrix_power(A,10)
Out[323]:
array([[89, 55],
[55, 34]])
Using the (newish) @ matrix multiplication operator, that's the same as:
In [324]: A@A@A@A@A@A@A@A@A@A
Out[324]:
array([[89, 55],
[55, 34]])
matrix_power does something more like:
In [325]: A2=A@A; A4=A2@A2; A8=A4@A4; A8@A2
Out[325]:
array([[89, 55],
[55, 34]])
And some comparative times:
In [326]: timeit np.linalg.matrix_power(A,10)
16.2 µs ± 58.1 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
In [327]: timeit M**10
33.5 µs ± 38.8 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
In [328]: timeit A@A@A@A@A@A@A@A@A@A
25.6 µs ± 914 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
In [329]: timeit A2=A@A; A4=A2@A2; A8=A4@A4; A8@A2
10.2 µs ± 97.9 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
numpy integers are implemented at int64, in c, so are limited in size. Thus we get overflow with a modest 100:
In [330]: np.linalg.matrix_power(A,100)
Out[330]:
array([[ 1298777728820984005, 3736710778780434371],
[ 3736710778780434371, -2437933049959450366]])
We can get around this by changing the dtype to object. The values are then Python ints, and can grow indefinately:
In [331]: Ao = A.astype(object)
In [332]: Ao
Out[332]:
array([[1, 1],
[1, 0]], dtype=object)
Fortunately matrix_power can cleanly handle object dtype:
In [333]: np.linalg.matrix_power(Ao,100)
Out[333]:
array([[573147844013817084101, 354224848179261915075],
[354224848179261915075, 218922995834555169026]], dtype=object)
Usually math on object dtype is slower, but not in this case:
In [334]: timeit np.linalg.matrix_power(Ao,10)
14.9 µs ± 198 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
I'm guessing it's because of the small (2,2) size of the array, where fast compiled methods aren't useful. This is basically an iterative task, where numpy doesn't have any advantages.
Scaling isn't bad - increase n by 10, and only get a 3-4x increase in time.
In [337]: np.linalg.matrix_power(Ao,1000)
Out[337]:
array([[70330367711422815821835254877183549770181269836358732742604905087154537118196933579742249494562611733487750449241765991088186363265450223647106012053374121273867339111198139373125598767690091902245245323403501,
43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875],
[43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875,
26863810024485359386146727202142923967616609318986952340123175997617981700247881689338369654483356564191827856161443356312976673642210350324634850410377680367334151172899169723197082763985615764450078474174626]],
dtype=object)
In [338]: timeit np.linalg.matrix_power(Ao,1000)
53.8 µs ± 83 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
With object dtype np.matrix:
In [340]: Mo = M.astype(object)
In [344]: timeit Mo**1000
86.1 µs ± 164 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
And for million, the times aren't as bad as I anticipated:
In [352]: timeit np.linalg.matrix_power(Ao,1_000_000)
423 ms ± 1.92 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
For comparison, the fastFibo times on my machine are:
In [354]: fastFibo(100)
Out[354]: 354224848179261915075
In [355]: timeit fastFibo(100)
3.91 µs ± 154 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
In [356]: timeit fastFibo(1000)
9.37 µs ± 23.2 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
In [357]: timeit fastFibo(1_000_000)
226 ms ± 12.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)