How do I plot two regression lines on the same plot with different x and y?-CodePudding

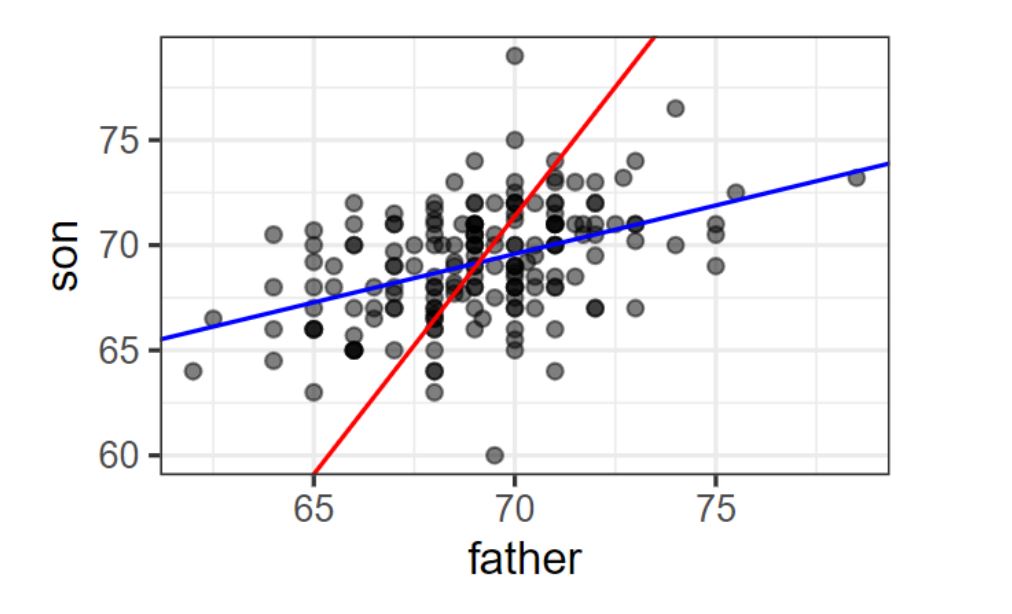
I am required to fit two simple linear regression lines, one with "y = father" and "x = son", the other with "y = son" and "x = father". I was able to do this with no issues and have gathered the correct equations. However, I am also required to plot them on the same scatterplot which is where I am running into some trouble. I am curious if there is a way I can plot the "y = father" and "x = son" regression line onto the scatterplot where y = son and x = father. Or is there a way I can combine the following two plots?

ggplot(galton_heights, aes(x = father, y = son))  
   geom_point()  
   geom_abline(slope = 0.46139, intercept = 37.28761, col = "blue")  
   theme_bw()

ggplot(galton_heights, aes(x = son, y = father))  
   geom_point()  
   geom_abline(slope = 0.40713, intercept = 40.93831, col = "red")  
   coord_flip()  
   theme_bw()

I was told my plot should look similar to this which is the two separate graphs I have above combined together.

CodePudding user response：

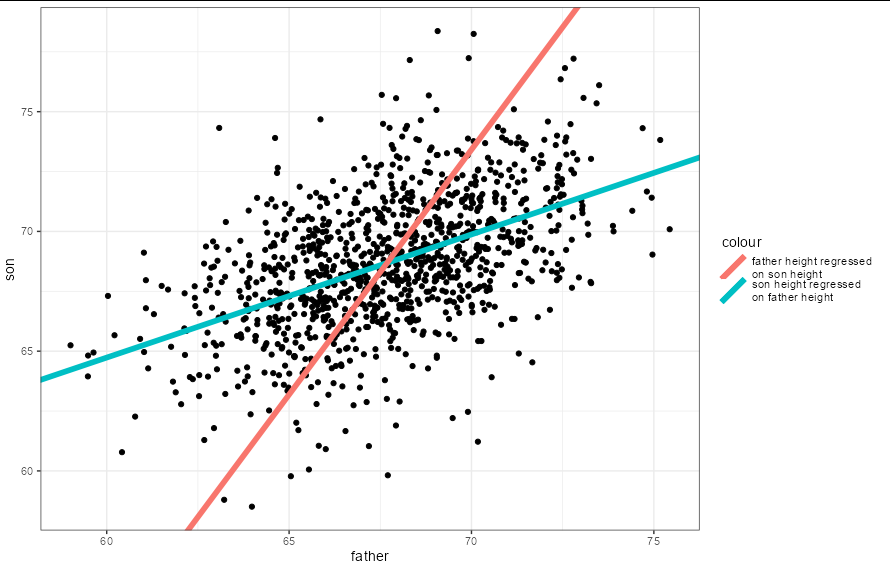
I think I may have a different set of data than you, but the principle is the same. Let's run a linear regression of son's heights on father's heights, then repeat it vice-versa

father_x <- lm(son ~ father, data = galton_heights)
son_x    <- lm(father ~ son, data = galton_heights)

coef(father_x)
#> (Intercept)      father 
#>   33.886604    0.514093

coef(son_x)
#> (Intercept)         son 
#>    34.10745     0.48890

Now, obviously the coefficients are different. The formula for son's heights based on father's heights is:

son = 0.514093 * father   33.886604

But if we take the other regression, we can rearrange it to solve for son's heights based on fathers' heights too:

father = 0.48890 * son   34.10745

son = (father - 34.10745)/0.48890

son = 2.045408 * father - 69.76365

This gives us plotting coefficients for our two lines:

ggplot(galton_heights, aes(x = father, y = son))  
   geom_point()  
   geom_abline(aes(slope = 0.514093, intercept = 33.886604, 
               colour = "son height regressed\non father height"),
               size = 2)  
   geom_abline(aes(slope = 2.045408, intercept = -69.76365, 
               color = "father height regressed\non son height"),
               size = 2)  
   theme_bw()

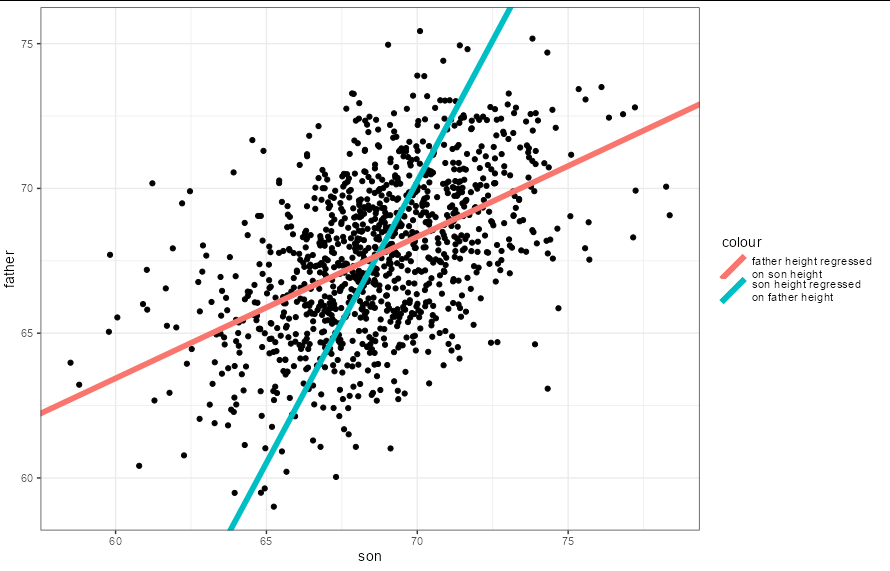
Notice the symmetry when we flip co-ordinates:

ggplot(galton_heights, aes(x = father, y = son))  
   geom_point()  
   geom_abline(aes(slope = 0.514093, intercept = 33.886604, 
               colour = "son height regressed\non father height"),
               size = 2)  
   geom_abline(aes(slope = 2.045408, intercept = -69.76365, 
               color = "father height regressed\non son height"),
               size = 2)  
   theme_bw()  
   coord_flip()

^{Created on 2022-02-12 by the reprex package (v2.0.1)}

CodePudding user response：

for the first part, you can simply use the geom_smooth to draw a linear regression line:

ggplot(galton_heights, aes(x = father, y = son))  
  geom_point()  
  geom_smooth(method = "lm", se = FALSE)  
  theme_bw

For the second part of the question, it doesn't really make sense to do it, as you should change the axis. You can do that:

ggplot(galton_heights, aes(x = father, y = son))  
  geom_point()  
  geom_smooth(method = "lm", se = FALSE, col = "blue")  
  geom_smooth(aes(y = father, x = son), method = "lm", se = FALSE, col = "red")  
 theme_bw()

But it is theoretically wrong.