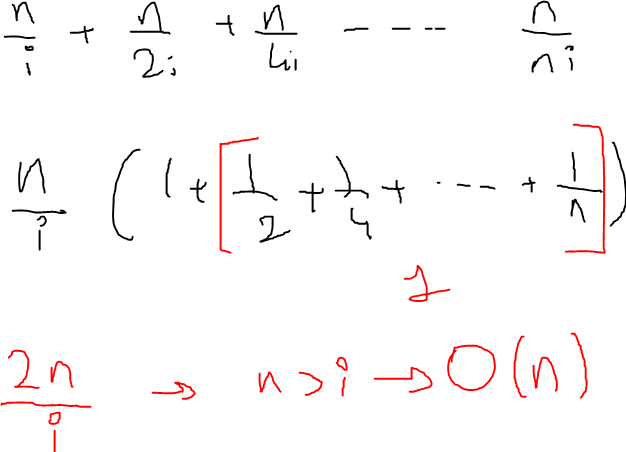What is time complexity of this algorithm ? (inner loop changes due to outer loop)-CodePudding

Algorithm(n):
   i = 1 , k = 0
   while i <= n {

    for (j = 1  to n/i){
        k = k 1
       }
    i = i * 2
   }

I understand outer loop works logn, i'm not sure but for inner loop it is working like n/i n/i/2 .. n/i/2^n . (it is not logn because We are updating i in outer loop)

i don't know how to combine them, because time complexity of inner loop changes at every loop.

Can anyone help me about this? What is the time complexity

CodePudding user response：

Actually i did some maths on this and it gave me the answer.

lets say n %2 = 0 and lets say 2^x = n and x is int.

for i = 1 -> n/i

for i = 2 -> n/2i

for i = 4 -> n/4i

for i = n -> n/ni

n/i ( 1 1/2 1/4 .. 1/n) and [1/2 1/4 ... 1/2^n] --> 1

n * 2/i --> n>i so the answer is O(n)

CodePudding user response：

The variable i in the outer loop takes on the values

i = 1, 2, 4, 8, ... X

where X is the smallest power of 2 larger than n (so X <= 2n).

For example, when n = 32:

i = 1, 2, 4, 8, 16, 32, 64.

Your inner loop runs n/i times (this might be rounded up or down, which is inconsequential here).

For example, when n = 32, the inner loop will run:

32/1   32/2   32/4   32/8   32/16   32/32   32/64
=
32   16   8   4   2   1   0
= 63 times

If you reverse the sum, you get the sum of all powers of 2 less than or equal to n, which is Theta(n) (at most 2n).