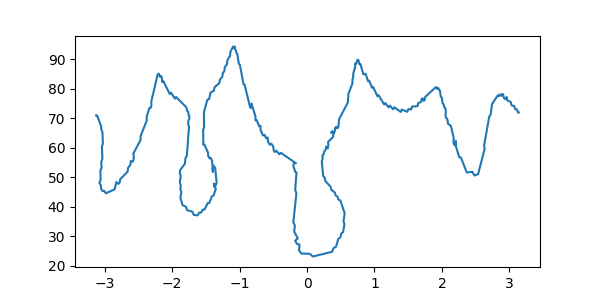
Convert image contours to polar coordinates-CodePudding

I'm trying to categorize the type of jigsaw puzzle pieces (number of heads, if it is a border or a corner...) by analyzing their contours.

The approach I'm trying to follow is analyzing this type of plot (from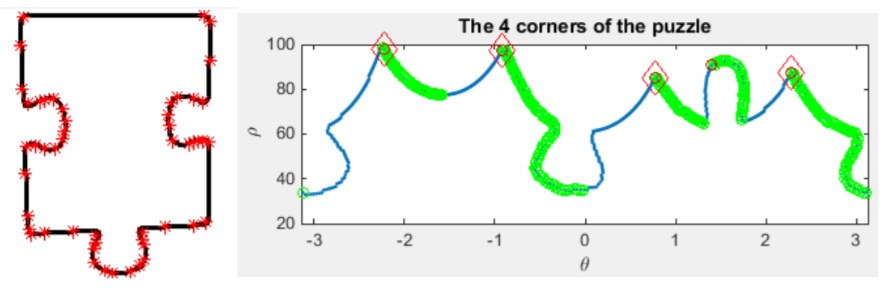

I've tried with:

import cv2
import matplotlib.pyplot as plt

def cart2pol(x, y):
    rho = np.sqrt(x**2   y**2)
    phi = np.arctan2(y, x)
    return(rho, phi)

# load image and find contours
img = cv2.imread("example.png", cv2.IMREAD_GRAYSCALE)
contours, _ = cv2.findContours(img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

# get contour points in polar coordinates
rhos = []
for i in range(len(contours[0])):
    x, y = contours[0][i][0]
    rho, _ = cart2pol(x, y)
    rhos.append(rho)

plt.show()
plt.plot(rhos)

but that produces a different plot, like this:

from this image:

Trying this on other images I can see how the peaks and valleys correspond to heads and holes of the pieces, but I would like a plot (not properly a function from what I see) like the one above. Can you help me to get that?

CodePudding user response：

Find the center of the tile:

M = cv2.moments(contours[0])
cx = int(M["m10"] / M["m00"])
cy = int(M["m01"] / M["m00"])

Calculate the vectors from the center to the points on the contour and convert the vectors to polar coordinates:

ds, phis = [], []
for i in range(len(contours[0])):
    x, y = contours[0][i][0]
    d, rho = cart2pol(x-cx, y-cy)
    ds.append(d)
    phis.append(rho)

Plot the polar coordinates with angle on the x-axis and distance on the y-axis:

plt.plot(phis, ds)

Complete example:

import os
os.chdir(os.path.abspath(os.path.dirname(__file__)))
import cv2
import matplotlib.pyplot as plt
import numpy as np

def cart2pol(x, y):
    rho = np.sqrt(x**2   y**2)
    phi = np.arctan2(y, x)
    return (rho, phi)

img = cv2.imread('opencv_so_9_example.png', cv2.IMREAD_GRAYSCALE)
contours, _ = cv2.findContours(img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

M = cv2.moments(contours[0])
cx = int(M["m10"] / M["m00"])
cy = int(M["m01"] / M["m00"])

polar = [cart2pol(c[0][0] - cx, c[0][1] - cy) for c in contours[0][:]]
max_i = polar.index(max(polar, key = lambda x: x[1]))
polar = polar[max_i:]   polar[:max_i]
ds, phis = zip(*polar)

plt.gcf().set_size_inches(6, 3)     
plt.plot(phis, ds)
plt.show()

CodePudding user response：

One can also do this with the binary image and warpPolar in Python/OpenCV.

Input:

import cv2
import numpy as np
import math

# read image
img = cv2.imread('puzzle.png')
ht, wd = img.shape[:2]

# convert to grayscale
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# threshold
thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY cv2.THRESH_OTSU)[1]

 # get non-zero points (i.e. white)
points = np.column_stack(np.where(thresh.transpose() > 0))

# get centroid
M = cv2.moments(points)
cx = int(M["m10"] / M["m00"])
cy = int(M["m01"] / M["m00"]) 

# compute maxradius = furthest corner - center
maxrad = math.sqrt( (wd-cx)*(wd-cx)   (ht-cy)*(ht-cy) )

# convert to polar image relative to centroid
polar1 = cv2.warpPolar(thresh, (ht,wd), (cx,cy), maxrad, cv2.INTER_CUBIC cv2.WARP_POLAR_LINEAR cv2.WARP_FILL_OUTLIERS)

# rotate 270 clocwise
polar2 = cv2.rotate(polar1, cv2.ROTATE_90_COUNTERCLOCKWISE)
ht, wd = polar2.shape[:2]

# save image
cv2.imwrite('puzzle_polar1.png',polar1)
cv2.imwrite('puzzle_polar2.png',polar2)

# show the images
cv2.imshow("polar1", polar1)
cv2.imshow("polar2", polar2)
cv2.waitKey(0)
cv2.destroyAllWindows()