Normal distribution `N(mu, 1)>1.96`-CodePudding

I try to write an R code to find value of mu s.t. the Normal distribution satisfies the probability P(N(mu, 1)>1.96)=0.95 (i.e., P(Z>1.96)=0.95 where Z~N(mu, 1) and mu is what I want to get). Is there any code for solving the parameter of distribution? It seems that this will be a integral equation about mu such that

int_{1.96}^{\infty} 1/\sqrt{2\pi} \exp(-(x-mu)^2/2)dx=0.95

We can sample Normal distribution from dnorm(x, mean, sd) or rnorm(n, mean, sd). But we need to first take value for mean and sd.

CodePudding user response：

Use uniroot to find the point where the probability equals 0.95. The function f is a way of writing this. The interval's end point are arbitrary, chosen because I wasn't not expecting the solution to be much faraway from the origin.
Note the argument lower.tail set to FALSE.

f <- function(x) {
  pnorm(1.96, mean = x, sd = 1, lower.tail = FALSE) - 0.95
}
uniroot(f, c(-5, 5))
#> $root
#> [1] 3.604879
#> 
#> $f.root
#> [1] 2.594975e-06
#> 
#> $iter
#> [1] 12
#> 
#> $init.it
#> [1] NA
#> 
#> $estim.prec
#> [1] 6.103516e-05

mu <- uniroot(f, c(-5, 5))$root
mu
#> [1] 3.604879

pnorm(1.96, mu, 1)
#> [1] 0.04999741
curve(pnorm(x, mu, 1),  from = -5, to = 8)
abline(h = 0.95, lty = "dashed")
abline(v = 1.96, lty = "dashed")

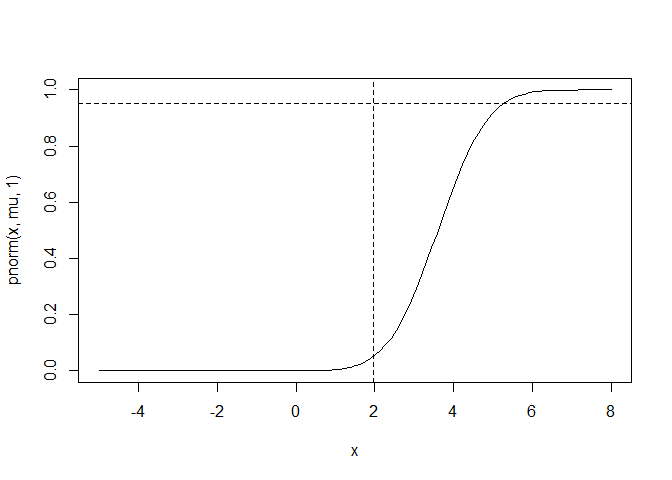
^{Created on 2022-02-28 by the reprex package (v2.0.1)}

CodePudding user response：

Here are some other options

Using qnorm uniroot (similar to the answer by @Rui Barradas)

> uniroot(function(m) qnorm(0.05, m) - 1.96, c(-1e3, 1e3))$root
[1] 3.604854

Using erfinv from pracma package

library(pracma)
> 1.96   sqrt(2) * pracma::erfinv(2 * 0.95-1)
[1] 3.604854