How to find the Final Path from the Traversal Path while performing BFS/DFS algorithm-CodePudding

I am trying to solve a problem which apples a Breadth-First Search Algorithm as well as Depth-First Search algorithm on a Tree and finds out the traversal and final paths that are found by both these algorithms.

What I am actually confused with is how do I calculate these two different paths? And are they really different?

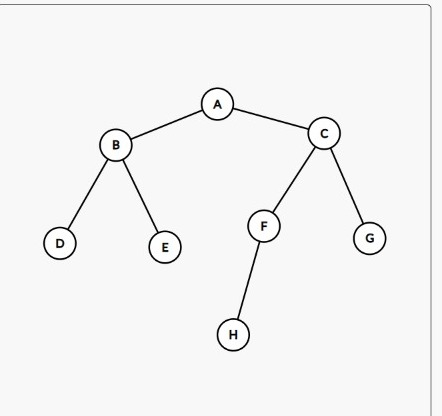
For example, consider the following tree,

Let's say, that our starting node is A and Goal node is H

For both the algorithms, this is what I feel would be the Traversed and Final Paths

For BFS

Traversal Path: A B C D E F G H

Final Path: A C F H

If this is how it works, then how can I find that Final Path? Its very easy to find traversed path, but not exactly so easy to find the Final Path.

Similarly,

For DFS

Traversal Path: A B D E C F G

Final Path: A C F H

Again, how can I extract the Final Path from the Traversal Path for DFS.

This actually gets a bit more complicated. What if my Goal Node is reachable from two sides? How do I find the Final Path in such a scenario?

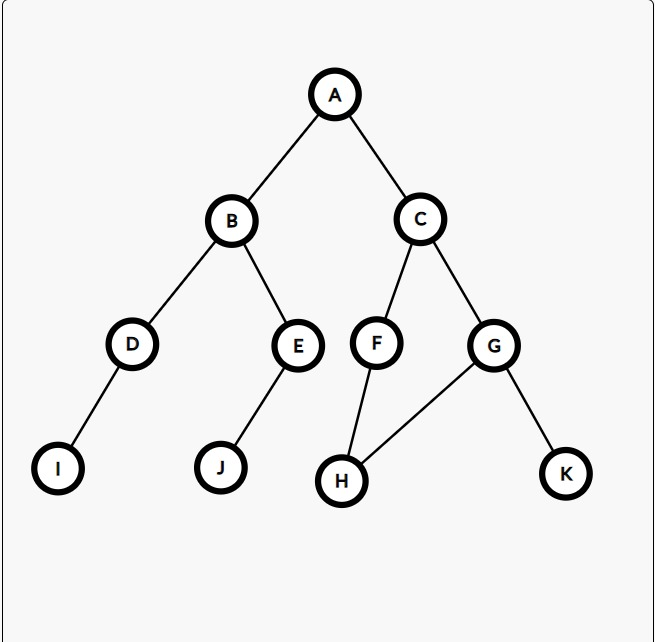
For example, Consider the following scenario,

Let's say for this case, our Starting Node is A and Goal Node is H, again.

Traversal path is very easy to compute with both BFS and DFS.

But for the Final Path, "H" is reachable from two sides, it is reachable from F and it is also reachable from G

For the DFS, you may write the final path as A C F G because from the F node, we would reach the H first (as G would still be unexplored, however you would still have to extract this Final Path from the Traversal path, which I do not know how to do)

But for BFS, you can not do that. So, what would be my Final Path in this scenario? Should there be two Final Paths in such a scenario?

Can anyone help me out in this please.

CodePudding user response：

One [out of many possible] approach is to maintain a map of target to source node. Every time you advance, record which source node was made to make that advance. So, in BFS case it will look like:

parents = {
  'A': NULL,
  'B': 'A',
  'C': 'A',
  'D': 'B',
  'E': 'B',
  'F': 'C',
  'G': 'C' 
}

Then, from the final node, reconstruct the path by going backward:

node = target
path = []
while node:
   path.append(node)
   node = parents[node]

Same approach works for DFS and Dijkstra