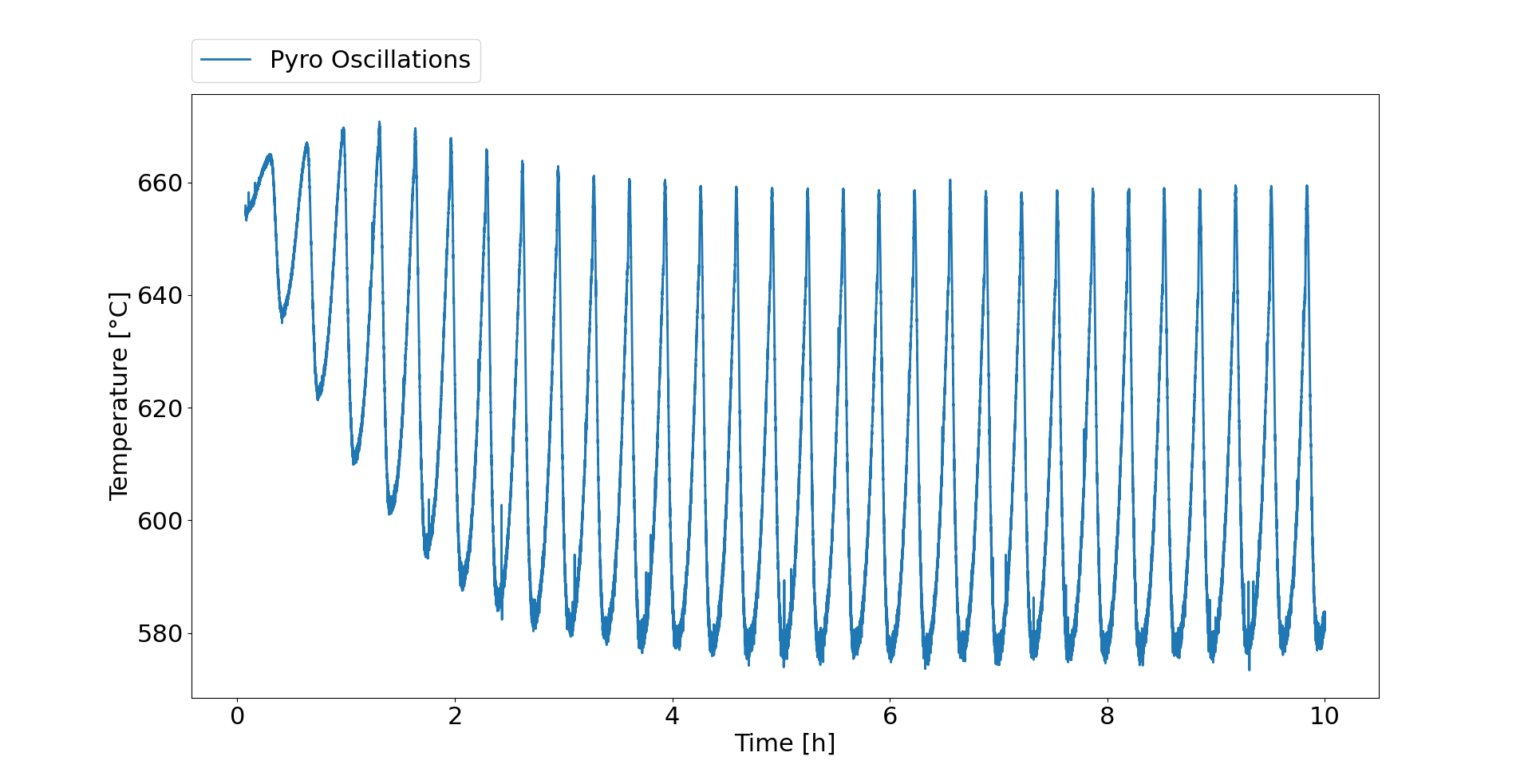
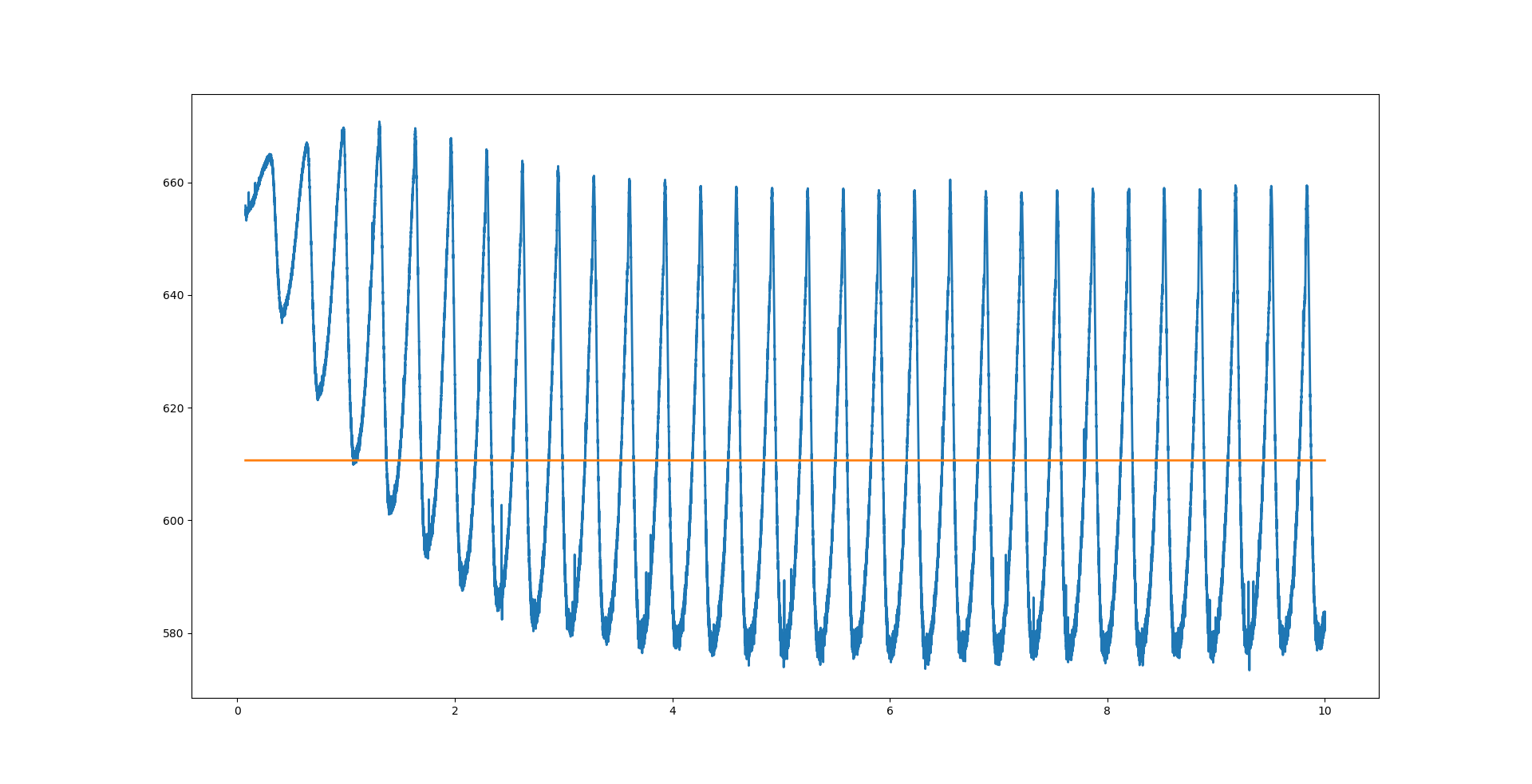
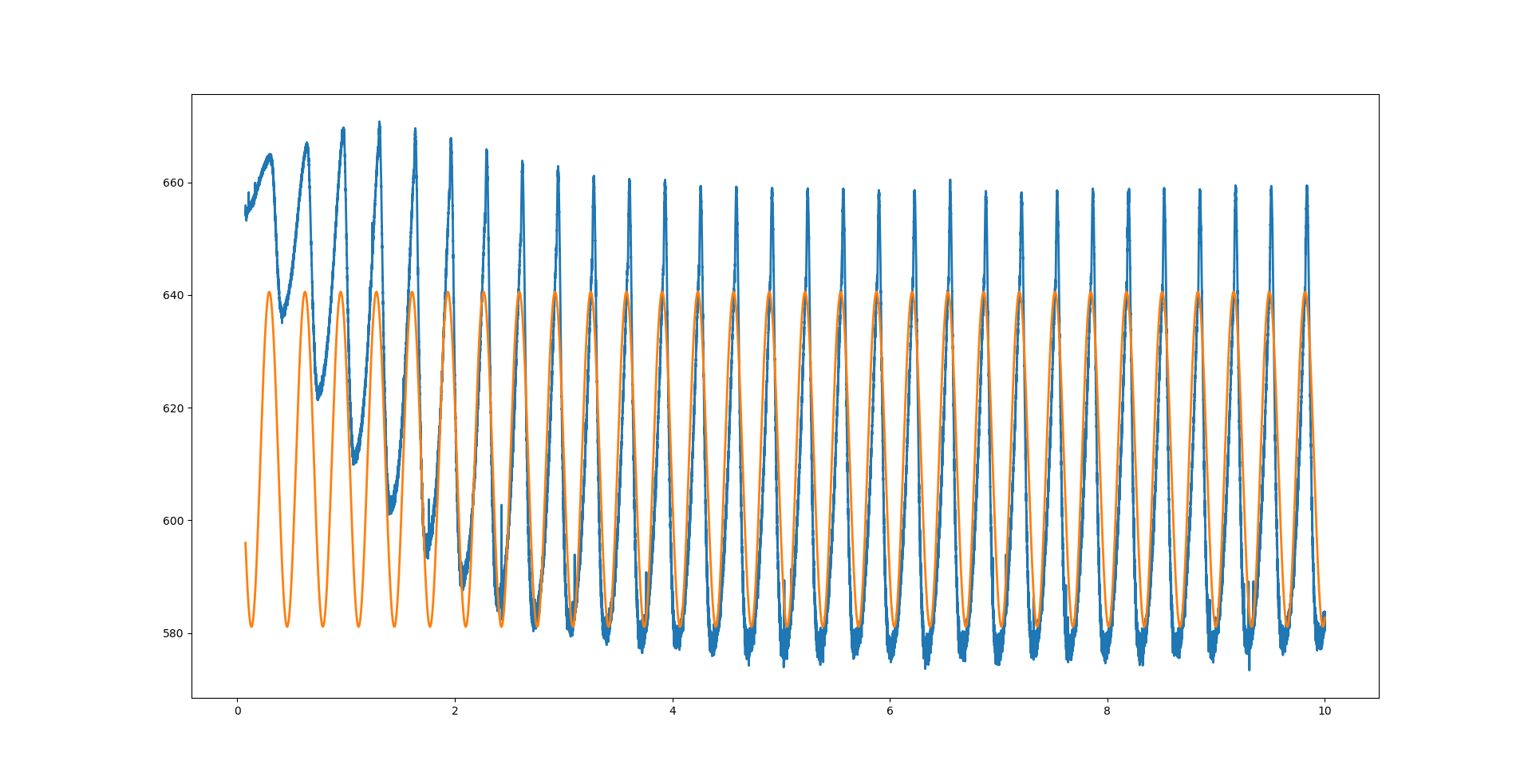
I am trying to fit experimental data

with a function of the form:

A * np.sin(w*t   p) * np.exp(-g*t)   c

However, the fitted curve (the line in the following image) is not accurate:

If I leave out the exponential decay part, it works and I get a sinus function that is not decaying:

The function that I use is from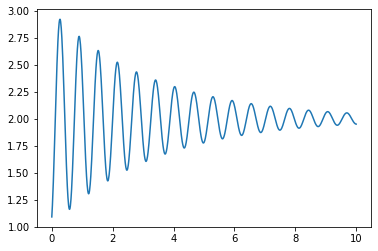

g stretches the envelope horizontally, c moves the center vertically, w determines the oscillation frequency, A stretches the envelope vertically.

So it can't accurately model the data you have.

Also, you will not be able to reliably fit w, to determine the oscilation frequency it is better to try an FFT.

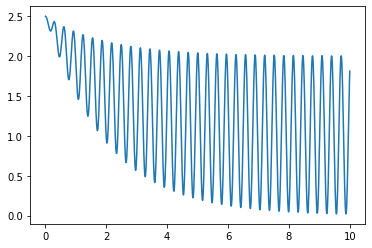
Of course you could adjust the function to look like your data by adding a few more parameters, e.g.

import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize
def sinfunc(t, A, w, p, g, c1, c2, c3):  return A * np.sin(w*t   p) * (np.exp(-g*t) - c1)   c2 * np.exp(-g*t)   c3

tt = np.linspace(0, 10, 1000)
yy = sinfunc(tt, -1, 20, 2, 0.5, 1, 1.5, 1)
plt.plot(tt, yy)

But you will still have to give a good guess for the frequency.