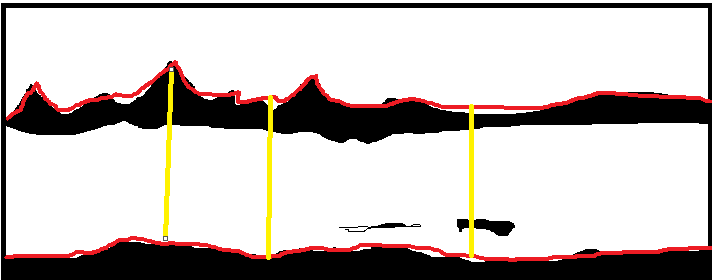
I want to find the distance between 2 irregular edges in a binary image. That is I have marked with red on the below image. My idea was to draw a colored line (say red) on both the edges and then calculate the distance between them at 10 equal intervals (yellow-colored marking)
I cropped the image into two. Say the top half is
Bottom half is
I want to draw the two red lines or just find the distance between those two somehow. I have been using OpenCV and PILLOW for a lot of steps.
there are also image instances where at few columns there are no black pixels in the top image. How do i calculate the distance of the black pixels only from the top? Just the top image.
CodePudding user response:
Here is one possible approach. I will leave the details to you. But the idea is to use Numpy argmax (or argmin as appropriate) to get the index of the first white after all black in each column. First I flip the image vertically so that the black is at the top. Numpy argmax, seems to find the first white value along the column.
Input (bottom image):
import numpy as np
import cv2
# read image
img = cv2.imread("img.png")
# Note that there is a 2 pixel tall white line at the bottom
# Note that there is columns of black at the left and right sides
# convert to grayscale
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# threshold
img = cv2.threshold(img,0,255,cv2.THRESH_BINARY)[1]
# flip vertically
img = cv2.flip(img, 0)
# remove 2 pixels at the top
img = img[2:, :]
# add one pixel row of white at bottom
img = cv2.copyMakeBorder(img, 0, 2, 0, 0, cv2.BORDER_CONSTANT, value=255)
# find max along each column
max = np.argmax(img, axis=0)
print(max.shape)
print(max)
cv2.imshow('flipped',img)
cv2.waitKey(0)
cv2.destroyAllWindows()
Here is the output:
(709,)
[112 112 112 112 32 32 32 32 32 32 32 32 32 32 32 32 32 32
31 31 31 31 31 31 31 31 31 31 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 31 31 31 31 31 31 31
31 31 31 31 31 31 31 31 31 30 30 30 30 30 30 30 30 30
30 30 30 31 31 32 32 33 33 34 35 35 36 36 36 36 36 36
36 36 36 36 36 36 36 36 37 37 38 38 39 39 39 40 40 40
41 41 43 43 44 45 45 46 46 46 46 46 46 46 46 46 46 46
46 46 46 46 46 46 46 46 46 46 46 46 46 45 45 45 45 44
44 44 44 44 44 44 44 44 44 44 44 44 43 43 43 43 43 43
43 43 43 43 43 43 43 44 44 44 44 44 44 44 44 43 43 43
42 42 42 42 42 42 42 42 42 42 41 41 40 40 40 40 40 40
40 40 40 40 40 40 40 40 40 40 40 40 39 39 39 39 39 39
39 39 39 39 39 39 39 39 39 39 39 39 38 38 37 37 37 37
37 37 37 36 36 36 36 36 35 35 35 34 34 34 34 34 34 34
34 34 33 33 32 32 32 32 32 32 32 32 32 32 32 32 32 32
33 33 34 34 35 35 36 37 37 37 37 38 38 38 38 38 38 38
38 38 38 38 38 38 38 39 39 40 40 40 40 40 39 39 39 39
39 39 38 38 38 37 37 37 37 37 37 37 37 37 37 37 37 37
37 38 38 38 39 40 40 41 41 41 39 39 38 37 37 37 37 37
37 37 37 37 37 37 37 37 37 37 37 37 37 37 37 37 38 38
38 39 39 39 39 39 39 39 39 41 41 41 41 41 41 41 41 41
41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41 41
40 40 40 40 40 40 40 40 40 40 39 39 38 38 37 37 37 37
36 36 36 36 36 36 35 35 34 34 34 33 33 33 32 31 31 31
31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31
31 31 31 31 31 31 31 31 30 30 29 29 29 28 28 28 28 27
27 26 26 26 26 26 26 26 26 26 26 26 26 26 26 27 27 27
27 27 27 27 27 27 28 28 28 28 28 28 28 28 28 28 28 28
28 28 28 28 28 28 28 28 28 28 28 28 28 28 29 29 29 29
29 29 29 29 29 29 29 29 29 29 29 29 29 29 29 29 29 29
29 28 28 27 27 27 27 27 27 27 27 27 27 27 27 27 28 28
28 28 29 29 30 30 30 31 31 32 32 33 33 34 34 35 35 36
36 36 37 37 37 38 38 39 39 39 39 39 39 39 39 39 39 39
39 38 38 37 37 37 37 37 37 36 36 35 35 35 35 35 35 35
35 35 35 35 35 35 35 35 35 35 35 36 36 36 36 36 36 36
36 36 36 36 36 36 37 37 37 37 37 37 37 37 37 37 37 37
37 37 37 37 37 37 37 37 37 37 37 37 37 37 37 37 37 37
37 37 37 37 37 37 37 37 37 37 37 37 37 37 37 37 37 37
37 37 37 37 37 37 37 37 37 37 37 37 37 38 38 38 39 39
39 39 39 40 112 112 112]