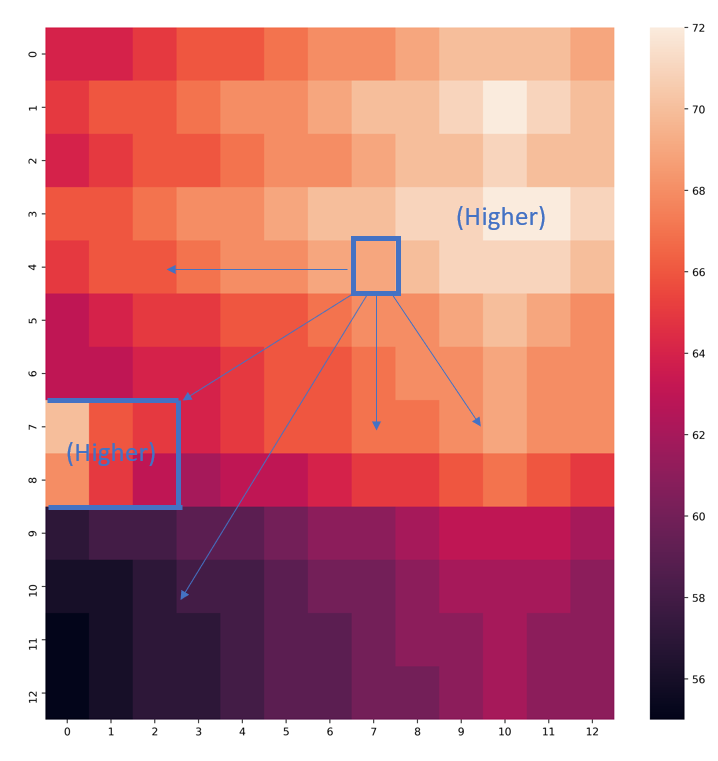
The below 2D numpy array represents a surface height. From any given cell in this matrix, I wish to find the cells which can be reached through continually moving away either flat (same height) or downhill (lower height). We can think of this as modelling where a ball could possibly roll if it is not allowed to roll back up any slope on the other side (no matter how small). Note the area to the left of the heatmap - it is lower than the target square but a trek uphill is still required to get there.
import numpy as np
arr_surface_2D = np.array([
[64, 64, 65, 66, 66, 67, 68, 68, 69, 70, 70, 70, 69],
[65, 66, 66, 67, 68, 68, 69, 70, 70, 71, 72, 71, 70],
[64, 65, 66, 66, 67, 68, 68, 69, 70, 70, 71, 70, 70],
[66, 66, 67, 68, 68, 69, 70, 70, 71, 71, 72, 72, 71],
[65, 66, 66, 67, 68, 68, 69, 69, 70, 71, 71, 71, 70],
[63, 64, 65, 65, 66, 66, 67, 68, 68, 69, 70, 69, 68],
[63, 63, 64, 64, 65, 66, 66, 67, 68, 68, 69, 68, 68],
[70, 66, 65, 64, 65, 66, 66, 67, 67, 68, 69, 68, 68],
[68, 65, 63, 62, 63, 63, 64, 65, 65, 66, 67, 66, 65],
[57, 58, 58, 59, 59, 60, 61, 61, 62, 63, 63, 63, 62],
[56, 56, 57, 58, 58, 59, 60, 60, 61, 62, 62, 62, 61],
[55, 56, 57, 57, 58, 59, 59, 60, 61, 61, 62, 61, 61],
[55, 56, 57, 57, 58, 59, 59, 60, 60, 61, 62, 61, 61]
]
)
If the array is 1 dimensional, I can come up with a not-very-elegant solution as follows, however I was thinking there is likely to be a more elegant solution which extends to 2D?
idx_target = 7
arr_surface_1D = np.array([
70, 66, 65, 64, 65, 66, 66, 67, # <-"target"
67, 68, 69, 68, 68])
# Slice array to the left side of idx_target, reverse direction to allow diff in next step
arr_left = arr_surface_1D[:idx_target][::-1]
# Determine number of spaces to the left where the values first start increasing
steps_left = np.argmax((np.diff(arr_left) > 0))
# Slice array to the right side of idx_target
arr_right = arr_surface_1D[idx_target 1:]
# Determine number of spaces to the right where the values first start increasing
steps_right = np.argmax((np.diff(arr_right) > 0))
arr_downhill = arr_surface_1D[idx_target-(steps_left 1):idx_target (steps_right)]
# Result is array array([64, 65, 66, 66])
CodePudding user response:
This is a path finding problem. It can be solved using a BFS (with a filtering on the explored neighbours regarding the heights of the source/destination cells). Some package like python-pathfinding may help you to do that. If you plan to implement this your self, note that you can speed it up using Numba (or Cython) since direct indexing in pure-Python is slow. This is certainly faster than using an existing package regarding your constraints.
Note that if you plan to do this on all cells, then I think there are faster algorithm based on drainage basins that can do that in (quasi-) linear time (in two passes). Doing a BFS would not be efficient in that case because of the re-computation of most cells.
CodePudding user response:
A modified flood fill algorithm finds the desired indices. Here is a pure (except representing 2D arrays with numpy) python implementation.
def downhill(arr, start):
q = [start]
fill = {start}
while q:
e = q.pop()
x, y = e
res = []
if x > 0: res.append((x-1, y))
if x < arr.shape[0]-1: res.append((x 1, y))
if y > 0: res.append((x, y-1))
if y < arr.shape[1]-1: res.append((x, y 1))
for p in res:
if p not in fill and arr[p] <= arr[e]:
q.append(p)
fill.add(p)
return np.array(tuple(fill))
x, y = downhill(arr_surface_2D, (4,7)).T
res = np.zeros_like(arr_surface_2D)
res[x,y] = 1
res
Output visualizing the indices as 1s in an array of 0s
array([[1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0],
[0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0],
[0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]])