Why is my loop taking forever to complete?-CodePudding

I am running an algorithm to generate normal distribution from 2 exponentials as follows:

set.seed(69420)
j = 1 
Z = c()

# Algorithm
while(j <= 10000){ Y1 <- rexp(1); Y2 <- rexp(1)
    if(Y2 - (Y1 -1)^2/2 >= 0 ){
            X = Y1
            U <- runif(1,0,1)
            if(U > 0.5){
                    Z[j] = X
            } else {
                    Z[j] = -X
            }
            j = j 1
    }
}

Then I am asked to modify the code as follows: "When we accept the sample Y1 (as X = Y1), the random variable Y = Y2 - (Y1 -1)2 / 2 also follows an exponential distribution with rate 1, and it is independent of Y1. Modify your code to recycle Y as one of the samples required."

I have written the following code to do the above task.

set.seed(69420)
j = 1
Z = c()
count = 0
Y2 <- rexp(1)
#Algorithm
while(j <= 50){
    Y1 <- rexp(1)
    Y = Y2 - (Y1 -1)^2/2
    if(Y >= 0){
        X = Y1
        Y2 = Y
        U <- runif(1,0,1)
        if(U > 0.5){
            Z[j] = X
        }else {
            Z[j] = -X
        }
        j = j 1
    }
    else if(Y < 0 & j == 1){
       Y2 <- rexp(1)
    }
}

However, my loop keeps running forever and even to produce 50 iterations it takes 5 mins. Is there anything I am doing wrong that is causing a long-running time? Also, can anyone suggest a method to vectorize the above code so my processing time can be reduced? Any help is appreciated.

Edit: Posting the whole question below for a better explanation.

Using the rejection method, we can generate samples from a standard Gaussian distribution N(0,1) using samples from an exponential distribution, Exp(1). The algorithm is as follows:

Generate Y1, Y2, independent samples from Exp(1).
If Y2 - (Y1 -1)^2 / 2 >= 0, set X = Y1. Otherwise, go back to step 1.
Generate a sample U from a uniform U(0,1). If U > 0.5, set Z = X. Otherwise, set Z = -X. The variable Z follows a Gaussian distribution.

a) Implement the algorithm in R. Provide your code in a separate file, rejection.R.

b) Generate 10000 samples of a Gaussian distribution using your code and report the sample mean and standard deviation.

c) Modify your code to count how many samples of the exponential and uniform distribution you need in order to obtain 10000 samples of a standard Gaussian. Run the code 10 times and report the average number of samples required.

d) When we accept the sample Y1 in step 2, the random variable Y = Y2 - (Y1 -1)2 / 2 also follows an exponential distribution with rate 1, and it is independent of Y1. Modify your code to recycle Y as one of the samples required in step 1. Submit your code in a separate file, rejection2.R.

e) Count how many samples is your code using now. Run the code 10 times and report the average number of samples required.

CodePudding user response：

I think you're being confused by the wording. The point is simply that you should harvest Y in the loop for each iteration, and it should be an exponentially distributed variable with mean of approximately 1:

set.seed(69420)
j = 1 
Z = c()
Y = c()

# Algorithm
while(j <= 10000){ Y1 <- rexp(1); Y2 <- rexp(1)
    if(Y2 - (Y1 -1)^2/2 >= 0 ){
            X = Y1
            Y[j] <- Y2 - (Y1 -1)^2 / 2
            U <- runif(1,0,1)
            if(U > 0.5){
                    Z[j] = X
            } else {
                    Z[j] = -X
            }
            j = j 1
    }
}

So Z should have a normal distribution:

hist(Z)

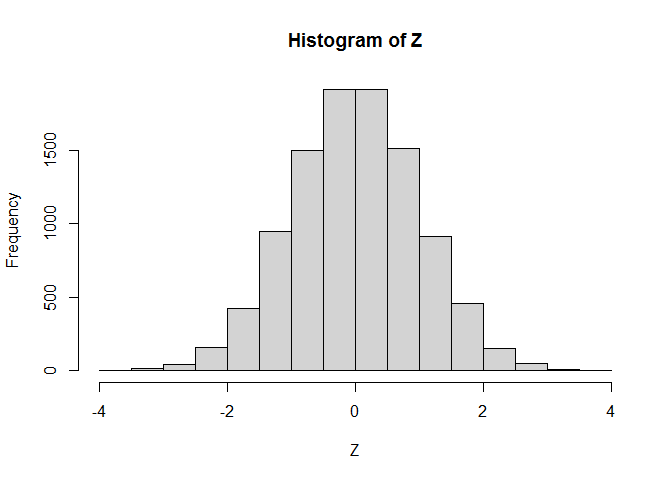
and Y an exponential distribution

hist(Y)

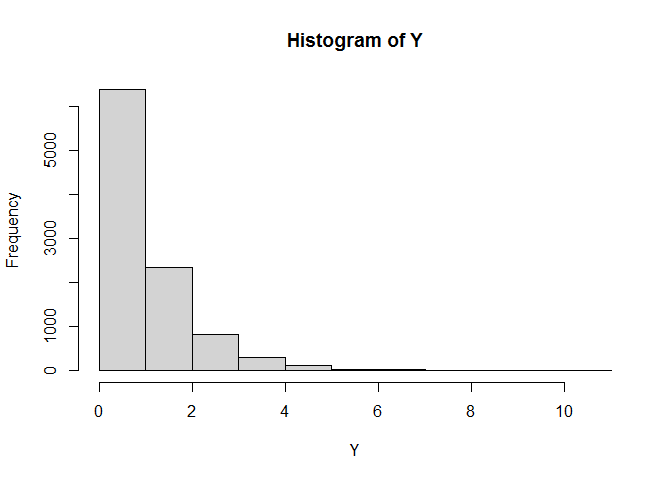
and the mean of Y should be close to 1:

mean(Y)
#> [1] 0.9870445

Edit

With further information from OP, the correct algorithm is simply to sample Y2 from an exponential distribution if Y is rejected:

set.seed(69420)
j = 1
Z = c()
count = 0
Y2 <- rexp(1)
#Algorithm
while(j <= 10000){
    Y1 <- rexp(1)
    Y = Y2 - (Y1 -1)^2/2
    if(Y >= 0){
        X = Y1
        Y2 = Y
        U <- runif(1,0,1)
        if(U > 0.5){
            Z[j] = X
        }else {
            Z[j] = -X
        }
        j = j 1
    }
    else {
       Y2 <- rexp(1)
    }
}

mean(Z)
#> [1] -0.00591165

sd(Z)
#> [1] 0.9961794

^{Created on 2022-03-27 by the reprex package (v2.0.1)}