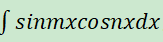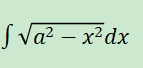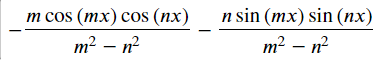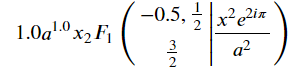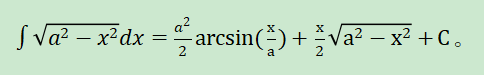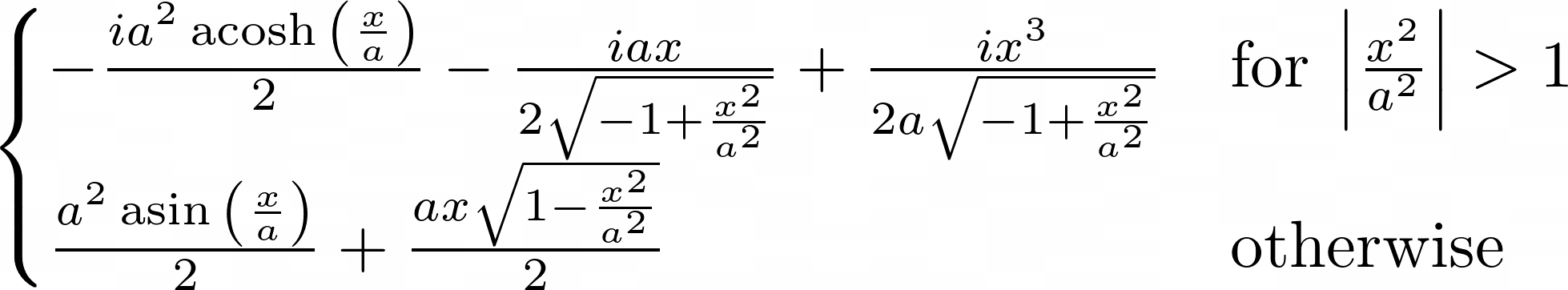Try to deal with simple inequilities in sympy integration-CodePudding

I'm trying to do some interesting integration problems for my Calculus I students under Anaconda python 3.8.5,

So question 1 is:

integrate(sin(m * x)* cos(n * x), x)

whereas x is the integration variable and m and n are 2 unequal and uncomplement (m != -n) real constants.

Question 2 is: integrate((a ** 2 - x ** 2) ** (1/2), x)

whereas for my Calculus I students we have to assume that |a| > |x| otherwise they won't be even able to interpret the results.

The following solution works for question 1:

m, n = symbols("m n", real=True, nonzero=True)
integrate(sin(m * x)* cos(n * x), x).args[2][0]

but for question 2 it obviously gives me results more than my Calculus I students can understand:

whereas I only want:

instread. Since I already know in question 1 that m!= n and m!=-n, and in question 2 |a| > |x|, is there a way that I can tell sympy this so that I don't have to dig through the Piecewise stuff (or to interpret the complex range result solutions) and get the answer directly? Thanks.

CodePudding user response：

If you want x > a, let's integrate from a to x with real variables:

>>> var('a x',positive=1)
(a, x)
>>> integrate((a ** 2 - x ** 2) ** (S.Half), (x,a,x))
a**2*asin(x/a)/2 - pi*a**2/4   x*sqrt(a**2 - x**2)/2

If you want to get rid of the constant you can do

>>> _.as_independent(x)[1]   Symbol("C")
C   a**2*asin(x/a)/2   x*sqrt(a**2 - x**2)/2

This will only change sign if x < a < 0, I b

CodePudding user response：

First of all, what version of SymPy are you using? You can verify that with:

import sympy as sp
print(sp.__version__)

If you are using older versions, maybe the solver is having trouble. The following solution has been tested on SymPy 1.9 and 1.10.1.

# define a, x as ordinary symbols with no assumptions. Sadly, it is not
# possible to make assumptions similar to |a| > |x|.
a, x = symbols("a, x")

# integrate the expression
res = integrate(sqrt(a**2 - x**2), x)
print(type(res))
# Piecewise

The result is a Piecewise object. As you can see, SymPy computed the complete solution. You can then extract the interested piece with the following command:

res.args[1][0]

Here, res.args[1] extracts the second piece, which is a tuple, (expr, condition). With res.args[1][0] we extract the expression from the second piece.