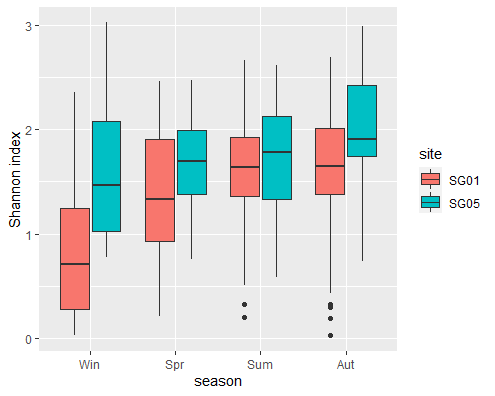
I have two sites and seasonal samples of plankton for each site. I have performed diversity indices for each season and site, and I have represented everything on the same plot using ggplot2 and geom_boxplot (I show you the plot).
These are the commands I used for the plot:
level_order <- c("Win", "Spr","Sum","Aut") #serve per cambiare l'ordine dei gruppi sull'asse delle x
ggplot(div, aes(x = factor(season, level = level_order), y = shannon)) geom_boxplot(aes(fill = site)) xlab("season") ylab("Shannon index")
What I would like to do now (and I am failing to), is have boxplot where the line is the mean of each group (e.g winter diversity of the first site and winter diversity of the second site) and a point is the median.
Any suggestions? Thank you in advance!!
I leave here an example of my div dataframe:
site season shannon
1 SG01 Win 1.55124832
2 SG01 Win 1.72057146
3 SG01 Spr 1.625478482
4 SG01 Spr 1.277293322
5 SG01 Sum 0.88550747
6 SG05 Sum 1.677666039
7 SG01 Sum 1.850984118
8 SG05 Sum 2.36108339
9 SG01 Aut 1.195804612
10 SG01 Aut 1.439432047
11 SG05 Aut 2.546555781
12 SG01 Win 0.284953317
13 SG05 Win 0.779162884
14 SG01 Spr 1.723890419
15 SG05 Spr 1.373792719
16 SG01 Sum 2.092365382
17 SG05 Sum 1.931014136
18 SG01 Sum 1.50502545
19 SG05 Sum 1.532379533
20 SG01 Aut 1.570949853
21 SG05 Aut 1.713710631
22 SG01 Aut 2.230091608
23 SG05 Aut 2.60573397
24 SG01 Win 0.876748429
25 SG05 Win 2.02200333
26 SG01 Win 2.352305681
27 SG01 Spr 1.891093419
28 SG05 Spr 1.394992271
29 SG01 Sum 1.946875957
30 SG05 Sum 1.599478879
31 SG01 Sum 2.124065518
32 SG05 Sum 1.515955871
33 SG01 Aut 1.158688215
34 SG05 Aut 1.748027849
35 SG01 Win 0.105111547
36 SG01 Spr 0.87617449
37 SG05 Spr 2.162793046
38 SG01 Spr 2.188259123
39 SG05 Spr 1.477570463
40 SG01 Spr 2.403560297
41 SG05 Spr 1.377893122
42 SG01 Sum 2.134173167
43 SG05 Sum 1.858323438
44 SG01 Sum 1.372338798
45 SG05 Sum 1.850782293
46 SG01 Sum 2.042722743
47 SG05 Sum 1.765405181
48 SG01 Sum 2.069671278
49 SG05 Sum 2.61192074
50 SG01 Aut 2.070530751
51 SG05 Aut 1.906772829
52 SG01 Aut 1.631107479
53 SG05 Aut 2.426254572
54 SG01 Win 1.987217164
55 SG05 Win 0.799496294
56 SG01 Spr 1.015641148
57 SG05 Spr 1.406142227
58 SG01 Spr 1.475127955
59 SG05 Spr 1.64170242
60 SG01 Sum 2.18855532
61 SG05 Sum 2.055605308
62 SG01 Sum 1.843388552
63 SG05 Sum 2.143056015
64 SG01 Aut 1.390632003
65 SG05 Aut 1.177005155
66 SG01 Win 0.436994857
67 SG05 Win 0.922177895
68 SG01 Win 0.111486445
69 SG05 Win 1.013003209
70 SG01 Spr 2.038485906
71 SG05 Spr 1.699342757
72 SG01 Spr 2.197461132
73 SG05 Spr 1.818752081
74 SG01 Spr 1.593323983
75 SG05 Spr 1.74058146
76 SG01 Sum 1.828585725
77 SG05 Sum 2.134304048
78 SG01 Sum 0.682908105
79 SG05 Sum 1.779730889
80 SG01 Sum 1.736418975
81 SG05 Sum 2.122669488
82 SG05 Aut 0.739529655
83 SG01 Aut 1.477379963
84 SG05 Aut 1.910292757
85 SG01 Aut 1.297295831
86 SG05 Aut 1.340215584
87 SG01 Win 0.607693424
88 SG05 Win 1.288681476
89 SG01 Win 1.123201233
90 SG05 Win 2.133970441
91 SG01 Win 2.087194385
92 SG05 Win 2.267827588
93 SG01 Spr 2.178855657
94 SG05 Spr 2.475019718
95 SG01 Spr 1.211745507
96 SG05 Spr 1.466358065
97 SG01 Spr 1.760959558
98 SG05 Spr 1.701252873
99 SG01 Sum 0.332361517
100 SG05 Sum 0.588153241
101 SG01 Sum 0.867165813
102 SG05 Sum 1.105468261
103 SG01 Sum 1.609437912
104 SG05 Sum 0.831497572
105 SG01 Aut 2.019695282
106 SG05 Aut 1.78876299
107 SG01 Aut 2.111590479
108 SG05 Aut 2.371876837
109 SG01 Aut 2.055512217
110 SG05 Aut 2.055472931
111 SG01 Aut 1.88461724
112 SG05 Aut 1.857836914
113 SG01 Win 0.849886275
114 SG05 Win 0.79030057
115 SG01 Sum 1.861445785
116 SG05 Sum 1.481311163
117 SG01 Sum 2.388759303
118 SG05 Sum 1.912778218
119 SG01 Aut 1.780059004
120 SG01 Aut 1.46783794
121 SG01 Win 0.162111238
122 SG01 Win 0.115561428
123 SG01 Win 0.063567551
124 SG01 Win 0.294800212
125 SG05 Win 0.831952782
126 SG01 Win 0.21439167
127 SG01 Win 1.411562768
128 SG01 Win 1.896814356
129 SG01 Win 1.038566269
130 SG01 Win 0.714502942
131 SG01 Spr 0.466288947
132 SG01 Spr 0.684086537
133 SG01 Spr 1.629302597
134 SG01 Sum 1.766008844
135 SG01 Sum 0.512330502
136 SG01 Sum 0.855249384
137 SG01 Sum 1.738085497
138 SG01 Sum 1.670846137
139 SG01 Sum 1.959151756
140 SG01 Sum 2.659931022
141 SG05 Sum 2.239514768
142 SG01 Aut 1.765273458
143 SG05 Aut 1.809746076
144 SG01 Aut 1.814669577
145 SG01 Aut 1.693459272
146 SG01 Aut 0.880029422
147 SG01 Aut 0.030424902
148 SG01 Aut 0.190036382
149 SG01 Win 0.028064827
150 SG01 Win 0.410753432
151 SG01 Win 1.196355197
152 SG01 Win 0.640028814
153 SG05 Win 2.172842158
154 SG01 Spr 0.310729618
155 SG01 Spr 0.431023204
156 SG01 Spr 1.957663797
157 SG05 Spr 1.819830757
158 SG01 Spr 0.399347092
159 SG01 Spr 1.298327832
160 SG05 Spr 2.011736101
161 SG01 Spr 0.76557657
162 SG01 Spr 2.127680798
163 SG01 Sum 1.990586223
164 SG01 Sum 1.176712496
165 SG01 Sum 1.163299687
166 SG01 Sum 1.342327775
167 SG05 Sum 1.45696041
168 SG01 Sum 1.425284821
169 SG01 Sum 0.603490683
170 SG05 Sum 0.8933049
171 SG01 Sum 0.832441299
172 SG01 Sum 0.203173153
173 SG01 Aut 0.432802137
174 SG01 Aut 0.689899451
175 SG01 Aut 0.633663257
176 SG01 Win 0.353839326
177 SG01 Win 0.060482006
178 SG01 Spr 0.212576264
179 SG01 Spr 1.593671964
180 SG05 Spr 1.17170529
181 SG01 Spr 2.37898595
182 SG01 Sum 1.557439793
183 SG05 Sum 1.468759607
184 SG01 Sum 0.723432071
185 SG05 Sum 1.24189285
186 SG01 Sum 1.633885941
187 SG01 Sum 1.970553561
188 SG05 Sum 2.568060749
189 SG01 Sum 1.390455469
190 SG01 Sum 1.489030655
191 SG01 Aut 1.877639964
192 SG05 Aut 2.17632569
193 SG01 Aut 1.805251144
194 SG01 Aut 2.398210416
195 SG05 Aut 1.52789825
196 SG01 Aut 1.781342289
CodePudding user response:
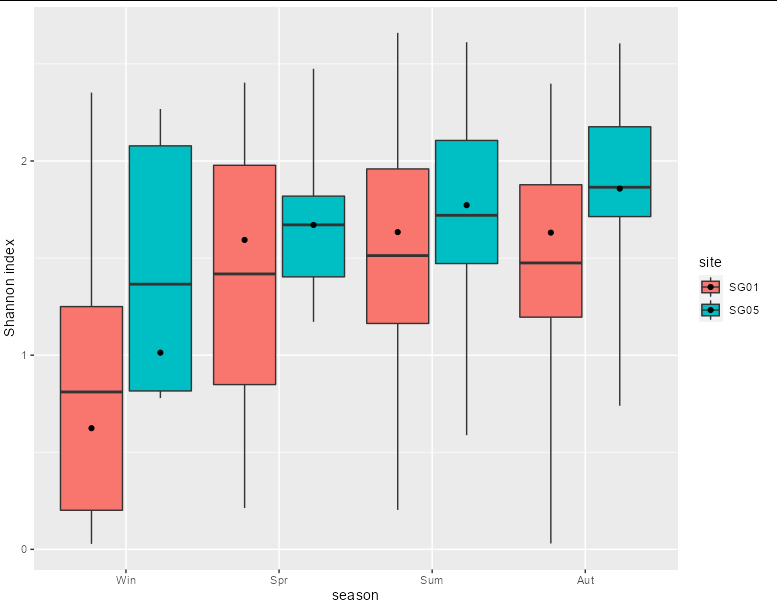
You can create the summary statistics beforehand and pass them through to geom_boxplot using stat = 'identity'
library(tidyverse)
div %>%
mutate(season = factor(season, level_order)) %>%
group_by(season, site) %>%
summarize(ymin = quantile(shannon, 0),
lower = quantile(shannon, 0.25),
median = median(shannon),
mean = mean(shannon),
upper = quantile(shannon, 0.75),
ymax = quantile(shannon, 1)) %>%
ggplot(aes(x = season, fill = site))
geom_boxplot(stat = 'identity',
aes(ymin = ymin, lower = lower, middle = mean, upper = upper,
ymax = ymax))
geom_point(aes(y = median, group = site),
position = position_dodge(width = 0.9))
xlab("season")
ylab("Shannon index")
CodePudding user response:
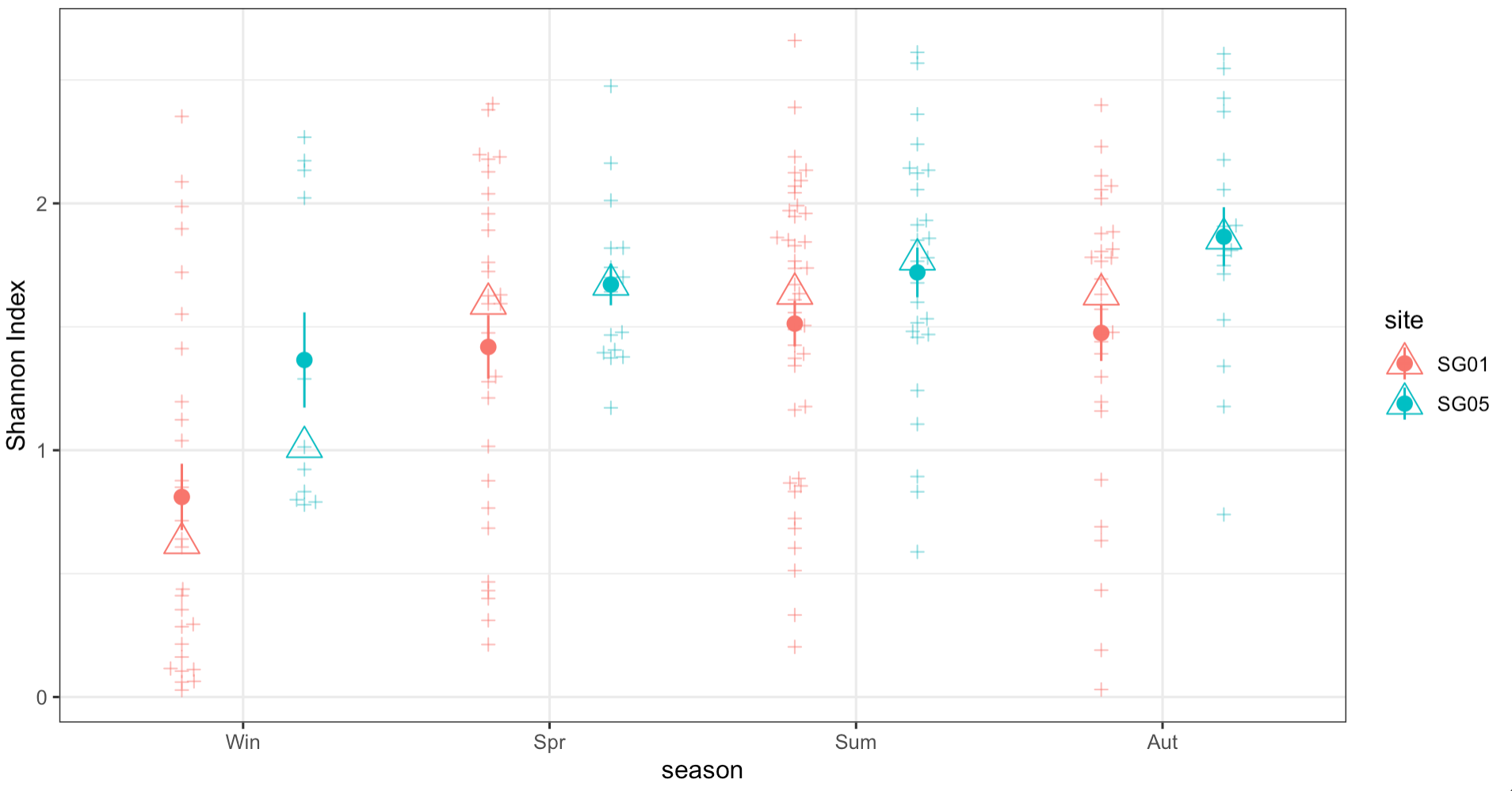
You could use stat_summary to create a new graph with the statistics you like. Since I think that having a "box" representing the "mean" would be a little bit confusing (because boxes on plots usually represent the quartiles) and because I am a believer in representing the actual datapoints, here is what I propose:
library(ggbeeswarm) # To add the data-points
ggplot(div, aes(x = factor(season, level = level_order),
y = shannon, color = site))
stat_summary(geom = "pointrange", # To add mean /- se
position = position_dodge(0.8))
stat_summary(geom = "point", # To add the median
fun = median,
position = position_dodge(0.8),
shape = 2, size = 5)
geom_beeswarm(dodge.width = 0.8, # To add the actual data points
alpha = 0.5, shape = 3)
labs(x = "season", y = "Shannon Index")
theme_bw()
And the result
Sorry I deviated from the question. If you really want boxes for the mean, replace "pointrange" by "crossbar" and if you think that the data-points are distracting, just remove the geom_beeswarm geometry.
Also, you can change the shape used for the median to one that you find prettier (Source: