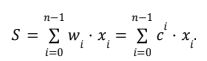Does anyone know how to solve this problem? It is easy to code this out to work in O(n^2) time complexity where you simply calculate the value of all possible combinations, but I'm unable to come up with an O(n) time complexity solution.

Given a list of integers x and a constant c, find the rotations of the list with the highest value and the lowest value respectively, where formula is:

and weights w = c^i, 0.2 <= c <= 0.8.

For example,

Input: x = [2,5,6,8] c = 0.8

Then possible rotations are

• 2 * 0.8**0 5 * 0.8**1 6 * 0.8**2 8 * 0.8**3 <-- Lowest value (13.936)
• 5 * 0.8**0 6 * 0.8**1 8 * 0.8**2 2 * 0.8**3
• 6 * 0.8**0 8 * 0.8**1 2 * 0.8**2 5 * 0.8**3 <-- Highest value (16.24)
• 8 * 0.8**0 2 * 0.8**1 5 * 0.8**2 6 * 0.8**3

Return: (13.936, 16.24)

Solve it in O(n) time complexity.

Here's my code:

def bounds_of_rotations(x,c):
    """ Time complexity of this method is O(n^2) since we are going through a list of size n for n times. 
    """
    upper_bound = ''
    lower_bound = ''
    
    for i in range(0,len(x)):
        value = 0
        for j in range(0, len(x)):
            index = (i j) % len(x)
            value  = x[index] * c**j
            
        if i == 0 or value > upper_bound:
            upper_bound = value
        if i == 0 or value < lower_bound:
            lower_bound = value
    
    return (lower_bound, upper_bound)

CodePudding user response：

There is a O(n) algorithm effectively. The idea is to build an array of size 2*n - 1:

{1*X[0] C*X[1] C^2*X[2] ... C^n-1*X[n-1] C^n*X[0] C^n 1*X[1] ... C^(2*n-2)* X[n-2]}

and to perform on it a sliding window sum calculation, wich can be implemented in O(2*n) = O(n).

The expected dot products are equal to the running sums, up to a weighting factor C^k.

Here is a simple C implementation, that could be easily transposed in any language.

#include <iostream>
#include <vector>
#include <utility>

std::pair<double, double> min_max_rotation (const std::vector<int>& X, double C) {
    int n = X.size();
    double vmin = 0.0, vmax = 0.0;
    double coef = 1.0;
    double sum = 0.0;
    std::vector<double> Xweighted (2*n);
    for (int i = 0; i < n;   i) {
        Xweighted[i] = X[i] * coef;
        sum  = Xweighted[i];
        coef *= C;
    }
    vmin = vmax = sum;
    double factor = C;
    for (int i = 0; i < n-1;   i) {
        Xweighted[i n] = X[i] * coef;
        coef *= C;
        sum  = (Xweighted[i n] - Xweighted[i]);
        double dot_product = sum / factor;
        factor *= C;
        if (dot_product < vmin) vmin = dot_product;
        if (dot_product > vmax) vmax = dot_product;
    }
    return {vmin, vmax};
}

int main() {
    std::vector<int> X = {2, 5, 6, 8};
    double C = 0.8;
    auto [vmin, vmax] = min_max_rotation (X, C);
    std::cout << vmin << "   " << vmax << "\n";
    return 0;
}