Efficient floating point scaling in C-CodePudding

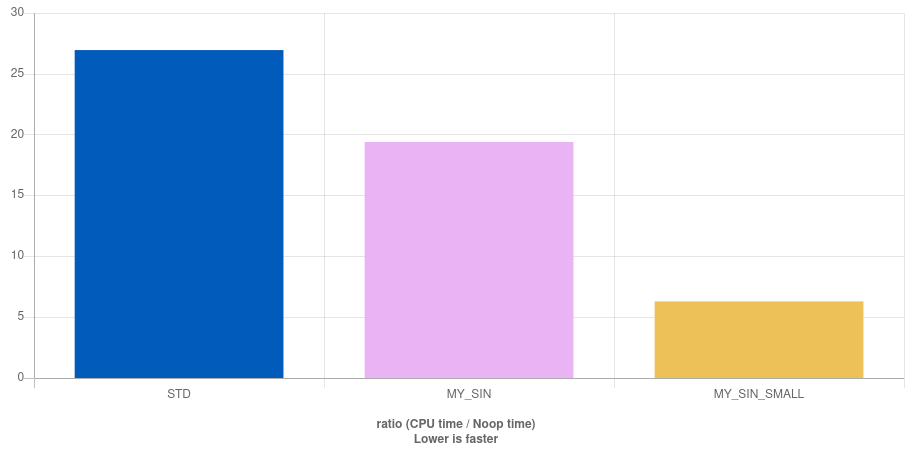
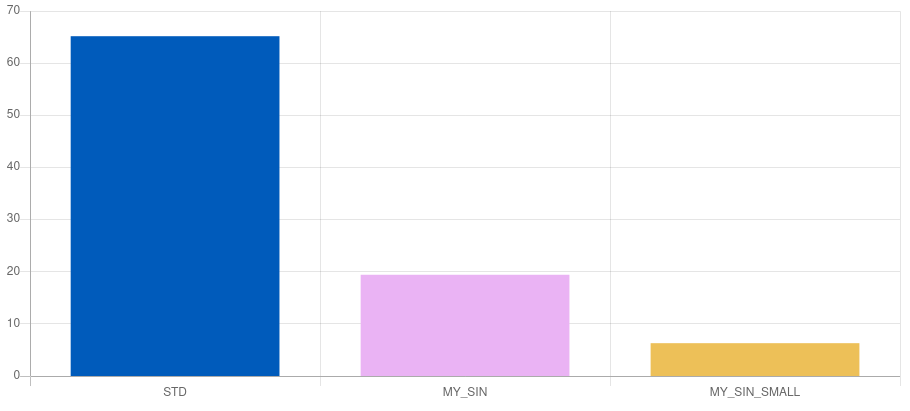
I'm working on my fast (and accurate) sin implementation in C , and I have a problem regarding the efficient angle scaling into the - pi/2 range.

My sin function for -pi/2 using Taylor series is the following (Note: FLOAT is a macro expanded to float or double just for the benchmark)

/**
 * Sin for 'small' angles, accurate on [-pi/2, pi/2], fairly accurate on [-pi, pi]
 */
// To switch between float and double
#define FLOAT float

FLOAT
my_sin_small(FLOAT x)
{
    constexpr FLOAT C1 = 1. / (7. * 6. * 5. * 4. * 3. * 2.);
    constexpr FLOAT C2 = -1. / (5. * 4. * 3. * 2.);
    constexpr FLOAT C3 = 1. / (3. * 2.);
    constexpr FLOAT C4 = -1.;
    // Correction for sin(pi/2) = 1, due to the ignored taylor terms
    constexpr FLOAT corr = -1. / 0.9998431013994987;

    const FLOAT x2 = x * x;

    return corr * x * (x2 * (x2 * (x2 * C1   C2)   C3)   C4);
}

So far so good... The problem comes when I try to scale an arbitrary angle into the -pi/2 range. My current solution is:

FLOAT
my_sin(FLOAT x)
{
    constexpr FLOAT pi = 3.141592653589793238462;
    constexpr FLOAT rpi = 1 / pi;

    // convert to  -pi/2 range
    int n = std::nearbyint(x * rpi);

    FLOAT xbar = (n * pi - x) * (2 * (n % 2) - 1);
    // (2 * (n % 2) - 1) is a sign correction (see below)
    return my_sin_small(xbar);
};

I made a

Benchmark results for double.

Sign correction for xbar in my_sin():

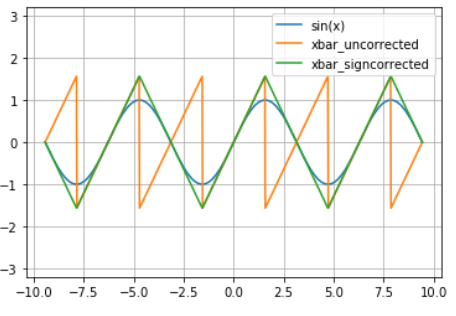
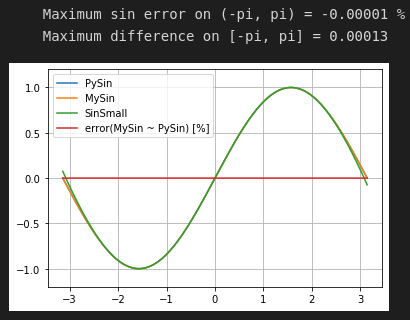
Algo accuracy compared to python sin() function:

CodePudding user response：


   FLOAT
   my_sin(FLOAT x)
   {
       constexpr FLOAT pi = 3.141592653589793238462;
       constexpr FLOAT rpi = 1 / pi;

       // convert to  -pi/2 range
       int n = std::nearbyint(x * rpi);

       FLOAT xbar = ((float)n * pi - x) * (2.0 * (n % 2.0) - 1.0);
       // (2 * (n % 2) - 1) is a sign correction (see below)
       return my_sin_small(xbar);
   };

Try 2.0 instead of 2

CodePudding user response：

((FLOAT)n % 2.0) or static_cast<FLOAT>n % 2.0