selecting data points neighbourhood to support vectors-CodePudding

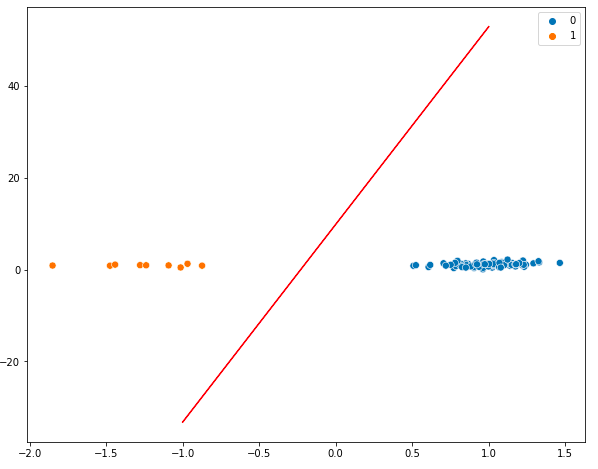
I have been thinking of this but not sure how to do it. I have a binary imbalanced data, and would like to use svm to select just subset of the majority data points nearest to support vector. Thereafter, I can fit a binary classifier on this "balanced" data.

To illustrate what I mean, a MWE:

# packages import
from collections import Counter
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
import numpy as np
from sklearn.svm import SVC
import seaborn as sns 

# sample data
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0,
    n_clusters_per_class=1, weights=[0.9], flip_y=0, random_state=1)

# class distribution summary
print(Counter(y))
Counter({0: 91, 1: 9})

# fit svm model 
svc_model = SVC(kernel='linear', random_state=32)
svc_model.fit(X, y)

plt.figure(figsize=(10, 8))

# Plotting our two-features-space
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y, s=50)

# Constructing a hyperplane using a formula.
w = svc_model.coef_[0]           # w consists of 2 elements
b = svc_model.intercept_[0]      # b consists of 1 element
x_points = np.linspace(-1, 1)    # generating x-points from -1 to 1
y_points = -(w[0] / w[1]) * x_points - b / w[1]  # getting corresponding y-points

# Plotting a red hyperplane
plt.plot(x_points, y_points, c='r')

The two classes are well separated by the hyperplane. We can see the support vectors for both classes (even better for class 1).

Since the minority class 0 has 9-data-points, I want to down-sample class 0 by selecting its support vectors, and 8 other data points nearest to it. So that the class distribution becomes {0: 9, 1: 9} ignoring all other data points of 0. I will then use this to fit a binary classifier like LR (or even SVC).

My question is how to select those data points of class 0 nearest to the class support vector, taking into account, a way to reach a balance with data points of minority class 1.

CodePudding user response：

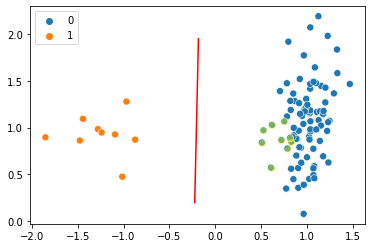
This can be achieved as follows: Get the support vector for class 0, (sv0), iterate over all data points in class 0 (X[y == 0]), compute the distances (d) to the point represented by the support vector, sort them, take the 9 with the smallest values, and concatenate them with the points of class 1 to create the downsampled data (X_ds, y_ds).

sv0 = svc_model.support_vectors_[0]
distances = []
for i, x in enumerate(X[y == 0]):
    d = np.linalg.norm(sv0 - x)
    distances.append((i, d))
distances.sort(key=lambda tup: tup[1])
index = [i for i, d in distances][:9]
X_ds = np.concatenate((X[y == 0][index], X[y == 1]))
y_ds = np.concatenate((y[y == 0][index], y[y == 1]))

plt.plot(x_points[19:-29], y_points[19:-29], c='r')
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y, s=50)
plt.scatter(X_ds[y_ds == 0][:,0], X_ds[y_ds == 0][:,1], color='yellow', alpha=0.4)