How can I use numpy to create a function that returns two-dimensional values from arrays of data?-CodePudding

This question is about deriving a mathematical function that returns pairs of values based on arrays of data - two-dimensional values from two-dimensional values.

I have created

From the x/y position of the pen, I obtain the required angles of the motors, and from that the pulse-widths that need to be fed to them.

These cheap motors are of course rather non-linear and the mechanical system as a whole exhibits hysteresis and distorting behaviours.

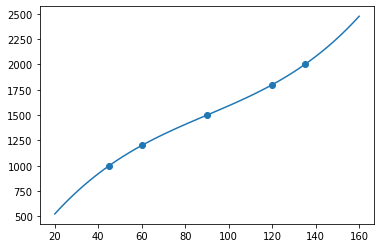
The library can calculate the required pulse-width values in different ways. One way is to determine some actual pulse-width/angle measurements for each servo, like so:

servo_angle_pws = [
    # angle, pulse-width
    [ 45, 1000],
    [ 60, 1200],
    [ 90, 1500],
    [120, 1800],
    [135, 2000],
]

and then

Now I'd like to take another step, and find a function in a similar way that gives me me the relationship between x/y positions and pulse-widths rather than angles (this will provide greater accuracy, as it will take into account more real-world imperfections in the system). In this case though, I will have two pairs of values, like this:

# x/y positions, servo pulse-widths
((-8.0,  8.0),  (1900, 1413)),
((-8.0,  4.0),  (2208, 1605)),
(( 8.0,  4.0),  ( 977, 1622)),
((-0.0,  4.0),  (1759, 1999)),
(( 6.0, 13.0),  (1065, 1121)),

My question is: what do I need to do to get a function (I'll need two of them of course) that returns pulse-width values for a desired pair of x/y positions? For example:

pw1 = xy_to_pulsewidths1(x=-4, y=6.3)
pw2 = xy_to_pulsewidths2(x=-4, y=6.3)

I believe that I need to do a "multivariate regression" - but I am no mathematician so I don't know if that's right, and even if it is, I have not yet found anything in my researches in numpy and scipy that indicates what I would actually need to do in my code.

CodePudding user response：

If I understand you correctly, you want to perform a multivariate regression, which is equivalent to solving a multivariate least-squares problem. Assuming your function is a 2D polynomial, you can use a combination of polyval2d and scipy.optimize.least_squares:

import numpy as np
from numpy.polynomial.polynomial import polyval2d
from scipy.optimize import least_squares

x = np.array((-8.0,-8.0, 8.0, -0.0, 6.0))
y = np.array((8.0, 4.0, 4.0, 4.0, 13.0))
pulse_widths = np.array(((1900, 1413),(2208, 1605),(977, 1622),(1759, 1999),(1065, 1121)))

# we want to minimize the sum of the squares of the residuals
def residuals(coeffs, x, y, widths, poly_degree):
    return polyval2d(x, y, coeffs.reshape(-1, poly_degree 1)) - widths

# polynomial degree
degree = 3

# initial guess for the polynomial coefficients
x0 = np.ones((degree 1)**2)

# res1.x and res2.x contain your coefficients
res1 = least_squares(lambda coeffs: residuals(coeffs, x, y, pulse_widths[:, 0], degree), x0=x0)
res2 = least_squares(lambda coeffs: residuals(coeffs, x, y, pulse_widths[:, 1], degree), x0=x0)

# Evaluate the 2d Polynomial at (x,y)
def xy_to_pulswidth(x, y, coeffs):
    num_coeffs = int(np.sqrt(coeffs.size))
    return polyval2d(x, y, coeffs.reshape(-1, num_coeffs))

# Evaluate the function
pw1 = xy_to_pulswidth(-4, 6.3, res1.x)
pw2 = xy_to_pulswidth(-4, 6.3, res2.x)