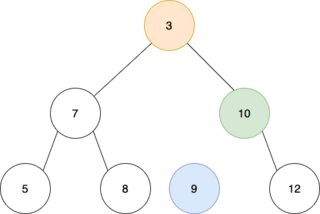
When removing a node from a binary search tree, you either replace the node with its biggest child on the left or its smallest child on the right.

I'm having a hard time understanding the way the following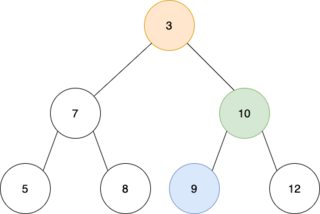

You call remove on the orange node:

• self is orange.
• replacement is the minimum of the right subtree - the blue node.

You recurse by calling remove on blue:

• self is blue
• replacement is nil as blue has neither left nor right children
• You call remove on nil (or rather you don't, because of the ?)
• Similarly, all of the other assignments are skipped because the optional values are all nil
• reconnectParent(node: nil) is called to fix the left/right linkage of blue's parent (this will result in green.left being assigned nil)
• You return blue

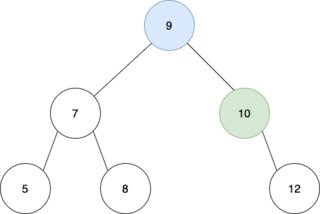
The tree now looks like:

You are now back out at the initial call to remove and execution continues. Remember,

• self is orange.
• replacement is blue node.

The next steps are:

• blue.right = orange.right
• blue.left = orange.left
• orange.right.parent = blue
• orange.left.parent = blue
• orange.reconnectParentTo(node:blue) - This does nothing since orange has no parent
• orange.parent = nil
• orange.right = nil
• orange.left = nil
• Return from remove - This was the initial call to remove, so we have exited all recursion

This leaves us with the final tree: