Find leading and trailing valleys adjacent to 1-D local maxima with Python-CodePudding

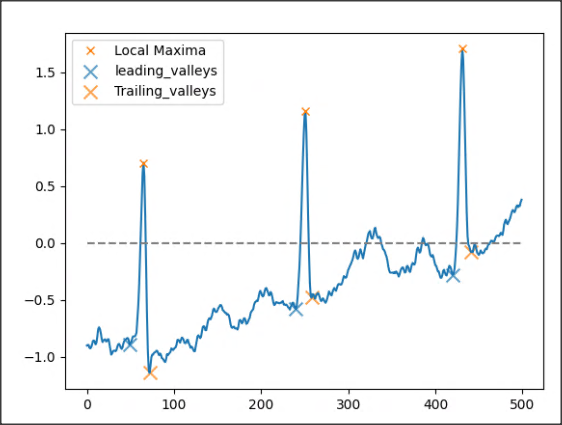
The objective is to find the leading and trailing valleys from a list of local maxima in a 1-D signal, as illustrated in the figure below

To do this,

I proposed to first find the peaks via the find_peaks of scipy.signal. This return a list of index where the local maxima occur.

Secondly, the signal.argrelextrema were employed to extract all the valleys. Finally, the third step is to select the closest boundary value pair (pair values from the valleys index) that each of the index from the find_peaks can reside.

While the code below works, but I am wondering whether there is more efficient way (can be Numpy of scipy) of doing this. I notice, the argrelextrema and searchsorted take some time for very long 1D signal

The full code to reproduce the above figure and

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy import signal
from scipy.misc import electrocardiogram
from scipy.signal import find_peaks

x = electrocardiogram()[2000:2500]

peaks, _ = find_peaks(x, height=0.7)

valley_indexes = signal.argrelextrema(x, np.less)[0]
i = np.searchsorted(valley_indexes, peaks)
m = ~np.isin(i, [0, len(valley_indexes)])

df = pd.DataFrame({'peaks_point': peaks})
df.loc[m, 'leftp'], df.loc[m, 'rightp'] = valley_indexes[i[m] - 1], valley_indexes[i[m]]



leftp=df['leftp'].to_numpy().astype(int)
rightp=df['rightp'].to_numpy().astype(int)


plt.plot(x)
plt.plot(peaks, x[peaks], "x",label='Local Maxima')

plt.scatter(leftp, x[leftp],marker='x',s=100,alpha=0.7,label='leading_valleys')
plt.scatter(rightp,x[rightp],marker='x',s=100,alpha=0.7,label='Trailing_valleys')

plt.plot(np.zeros_like(x), "--", color="gray")
plt.legend()
plt.show()

CodePudding user response：

I don't think there's a faster way to do this using just numpy/scipy. The obvious optimization is to stop searching at the first local minimum around the peaks. Unfortunately, this is slower on the example input when written in pure python (at least until the intermediate arrays in the argrelextrema method fill up my RAM).

If you can use numba, though, this optimization is much faster:

10800000 points, 98900 peaks (54.29 ms for peaks):
argrelextrema:    143.04 ms
optimized python: 572.55 ms
optimized numba:    8.04 ms

import time
import numpy as np
from numba import jit
from scipy import signal
from scipy.misc import electrocardiogram
from scipy.signal import find_peaks

def argrelextrema(arr, peaks):
    valley_indexes = signal.argrelextrema(arr, np.less)[0]
    i = np.searchsorted(valley_indexes, peaks)
    m = ~np.isin(i, [0, len(valley_indexes)])
    return valley_indexes[i[m] - 1], valley_indexes[i[m]]

def find_neighboring_valleys(arr, peak_idx):
    right = -1
    for i in range(peak_idx   1, len(arr) - 1):
        if arr[i - 1] > arr[i] < arr[i   1]:
            right = i
            break
    left = -1
    for i in range(peak_idx - 1, 0, -1):
        if arr[i - 1] > arr[i] < arr[i   1]:
            left = i
            break
    return left, right

def optimized_python(arr, peaks):
    lefts = np.empty_like(peaks)
    rights = np.empty_like(peaks)
    for i, peak in enumerate(peaks):
        lefts[i], rights[i] = find_neighboring_valleys(arr, peak)
    return lefts, rights

find_neighboring_valleys_numba = jit(find_neighboring_valleys)

@jit
def optimized_numba(arr, peaks):
    lefts = np.empty_like(peaks)
    rights = np.empty_like(peaks)
    for i, peak in enumerate(peaks):
        lefts[i], rights[i] = find_neighboring_valleys_numba(arr, peak)
    return lefts, rights


x = np.tile(electrocardiogram(), 100)

start = time.perf_counter()
peaks, _ = find_peaks(x, height=0.7)
elapsed = time.perf_counter() - start
print(f"{len(x)} points, {len(peaks)} peaks ({elapsed*1000:.2f} ms for peaks):")

start = time.perf_counter()
leftp, rightp = argrelextrema(x, peaks)
elapsed = time.perf_counter() - start
print(f"argrelextrema:    {elapsed*1000:6.2f} ms")

start = time.perf_counter()
leftp, rightp = optimized_python(x, peaks)
elapsed = time.perf_counter() - start
print(f"optimized python: {elapsed*1000:6.2f} ms")

# warmup the jit
optimized_numba(x, peaks)
start = time.perf_counter()
leftp, rightp = optimized_numba(x, peaks)
elapsed = time.perf_counter() - start
print(f"optimized numba:  {elapsed*1000:6.2f} ms")

CodePudding user response：

Another approach is to first invert the x which invert the valley as a peak.

peaks_valley, _ = find_peaks(x*-1, height=0)

and select the closest boundary value pair (pair values from the valleys index) that each of the index from the find_peaks can reside.

The full code together with the comparison with the argrelextrema is as below:

import time

import numpy as np
import pandas as pd
from scipy import signal
from scipy.misc import electrocardiogram
from scipy.signal import find_peaks


def _get_vally_idx_pd(valley_indexes, peaks):
    i = np.searchsorted(valley_indexes, peaks)
    m = ~np.isin(i, [0, len(valley_indexes)])

    df = pd.DataFrame({'peaks_point': peaks})
    df.loc[m, 'leftp'], df.loc[m, 'rightp'] = valley_indexes[i[m] - 1], valley_indexes[i[m]]
    return df

def argrelEx_approach(peaks,x):
    valley_indexes = signal.argrelextrema(x, np.less)[0]
    df=_get_vally_idx_pd(valley_indexes, peaks)
    print(df)

def _invert_approach(peaks,x):
    peaks_valley, _ = find_peaks(x*-1, height=0)
    df=_get_vally_idx_pd(peaks_valley, peaks)
    print(df)

x = electrocardiogram()[2000:2500]

peaks, _ = find_peaks(x, height=0.7)


start1 = time.perf_counter()
argrelEx_approach(peaks,x)
end1 = time.perf_counter()
time_taken = end1 - start1
start2 = time.perf_counter()
_invert_approach(peaks,x)
end2 = time.perf_counter()
    
print('Time to complete argrelextrema : ',end1 - start1)
print('Time to complete inverting the signal: ',end2 - start2)

Output

Time to complete argrelextrema :  0.004720643861219287
Time to complete inverting the signal:  0.0034988040570169687

Which is also still faster than the suggestion by yut23.