Mixture Poisson distribution: mean and variance in R-CodePudding

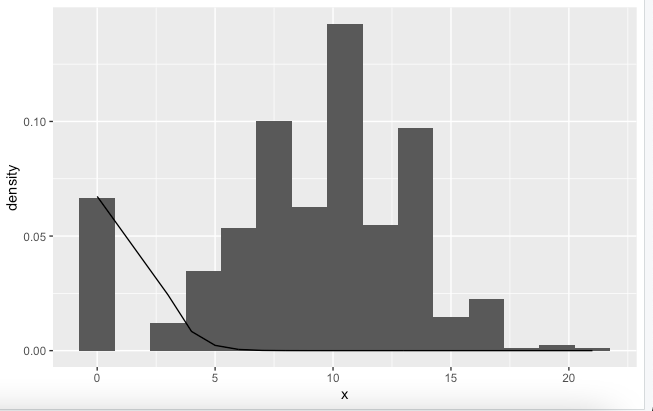
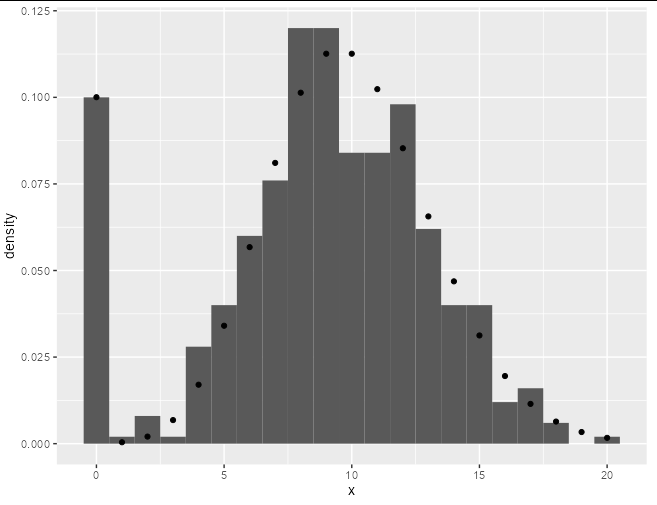
So, I tried to simulate mixed Poisson distribution:

data2 <- data.frame(x = c(rpois(n = 50, lambda = 0), rpois(n = 450, lambda = 10)))

Then plot the histogram and density function upon it, for the distribution function I used function dmixpois from spatstat package. Here is the code for the plot:

ggplot(data2, aes(x = x))  
  geom_histogram(aes(y = ..density..), bins = 15)  
  geom_line(aes(x = x, y = dmixpois(data2$x, mu = 9, sd = sqrt(41))))

Here is the plot:

Clearly, the density function is wrong. As far as I know, the mean for mixed Poisson distribution is linear combination of the means for the singled distributions and the variance is E[lambda] Var[lambda]. Here on the plot I only used the variance term, but if I add the expected value of lambda, I get the density to be even more steep. What is wrong with the computations?

CodePudding user response：

The 'mixed Poisson' that you are simulating isn't the same as the mixed Poisson model in spatstat, which just assumes that the lambda of a Poisson distribution itself is a normally-distributed random variable. From the docs:

In effect, the Poisson mean parameter lambda is randomised by setting lambda = invlink(Z) where Z has a Gaussian N(μ,σ²) distribution.

It therefore won't simulate the mixing of two independent Poisson distributions.

It looks like what you are simulating is a zero-inflated Poisson distribution, that is to say, a distribution where there is a probability of getting zero counts or a Poisson-distributed count for any given observation. There is a specific dzipois for this in the VGAM package.

Remember also that a Poisson distribution is a discrete probability distribution, so you cannot properly show it with a continuous line, but rather only with points or spikes at the integer values.

If you want to plot a distribution that matches your simulation, you can try the following:

set.seed(1) # To make the example reproducible

data2 <- data.frame(x = c(rpois(n = 50, lambda = 0), 
                          rpois(n = 450, lambda = 10)))


ggplot(data2)  
  geom_histogram(aes(x = x, y = ..density..), breaks = 0:21 - 0.5)  
  geom_point(data = data.frame(x =0:20, y = VGAM::dzipois(0:20, 10, 1/10)),
             aes(x, y))

CodePudding user response：

First of all the Poisson distribution with lambda = 0 is degenerate and always constant to zero:

rpois(10, lambda = 0)
[1] 0 0 0 0 0 0 0 0 0 0

This is why you have a spike at x = 0.

Second, the Poisson distribution is discrete and as such does not have a density (or pdf). Instead you can plot the relative frequencies in histogram (as you did) to get an estimation for the probability of X = x.

The mean of the mixed distribution is simply the weighted mean of the underlying distributions. In your case the underlying distribution have weights 10% and 90% and hence E[X] = 0.1 E[X_1] 0.9 E[X_2] = 0,9

The variance of the mixed distribution is given by Var(X) = Var(\Lambda) E[Lambda]

So everything is working as it should:

set.seed(1)

df <- data.frame(x = c(rpois(50, 1), rpois(450, 9))) 

mean(df$x)
sd(df$x)
var(df$x)