Create an area plot where each area is evenly filled with the actual number of points?-CodePudding

I'd like to create a graph like the one below. It's kind of a combination of using geom_area and geom_point.

Let's say my data looks like this:

library(gcookbook, janitor)

ggplot(uspopage, aes(x = Year, y = Thousands, fill = AgeGroup))  
    geom_area()

I obtain the following graph

Then, I'd like to add the exact number of points as the total for each category, which would be:

library(dplyr)
uspopage |> 
    group_by(AgeGroup) |> 
    summarize(total = sum(Thousands))

# A tibble: 8 × 2
  AgeGroup   total
  <fct>      <int>
1 <5       1534529
2 5-14     2993842
3 15-24    2836739
4 25-34    2635986
5 35-44    2331680
6 45-54    1883088
7 55-64    1417496
8 >64      1588163

CodePudding user response：

Following some twitter comments my workaround is as follows:

1 - create the original plot with ggplot2

2 - grab the areas of the plot as a data.frame (ggplot_build)

3 - create polygons of the points given in 2, and make it a sensible sf object (downscale to a flatter earth)

4 - generate N random points inside each polygon (st_sample)

5 - grab these points and upscale back to the original scale

6 - ggplot2 once again, now with geom_point

7 - enjoy the wonders of ggplot2

library(gcookbook)
library(tidyverse)
library(sf)

set.seed(42)

# original data
d <- uspopage

# number of points for each group (I divide it by 1000)
d1 <- d |> 
    group_by(AgeGroup) |> 
    summarize(n_points = round(sum(Thousands) / 1e3)) |> 
    mutate(group = 1:n())

# original plot
g <- ggplot(data = d, 
       aes(x = Year, 
           y = Thousands, 
           fill = AgeGroup))  
    geom_area()

# get the geom data from ggplot
f <- ggplot_build(g)$data[[1]]

# polygons are created point by point in order. So let´s, by group, add the data.frame back to itself first part is the ymin line the secound the inverse of ymax line (to make a continous line from encompassing each area).

# list of groups
l_groups <- unique(f$group)

# function to invert and add back the data.frame
f_invert <- function(groups) {
  k <- f[f$group == groups,]
  k$y <- k$ymin
  
  k1 <- k[nrow(k):1,]
  k1$y <- k1$ymax
  
  k2 <- rbind(k, k1)
  
  return(k2)
}

# create a new data frame of the points in order
f1 <- do.call("rbind", lapply(l_groups, f_invert))

# for further use at the end of the script (to upscale back to the original ranges)
max_x <- max(f1$x)
max_y <- max(f1$y)
min_x <- min(f1$x)
min_y <- min(f1$y)

# normalizing: limiting sizes to a fairy small area on the globe (flat earth wannabe / 1 X 1 degrees)
f1$x <- scales::rescale(f1$x)
f1$y <- scales::rescale(f1$y)

# create polygons
polygons <- f1 |>
  group_by(group) |> 
  sf::st_as_sf(coords = c("x", "y"), crs = 4326) |>
  summarise(geometry = sf::st_combine(geometry)) |>
  sf::st_cast("POLYGON")

# cast N number of points randomly inside each geometry (N is calculated beforehand in d1)
points <- polygons %>% 
    st_sample(size = d1$n_points,
              type = 'random', 
              exact = TRUE) %>% 
    # Give the points an ID
    sf::st_sf('ID' = seq(length(.)), 'geometry' = .) %>% 
    # Get underlying polygon attributes (group is the relevant attribute that we want to keep)
    sf::st_intersection(., polygons)

# rescale back to the original ranges
points <- points |>
   mutate(x = unlist(map(geometry,1)),
          y = unlist(map(geometry,2))) |>
   mutate(x = (x * (max_x - min_x)   min_x),
          y = (y * (max_y - min_y)   min_y))

# bring back the legends
points <- left_join(points, d1, by = c("group"))

# final plot
g1 <- ggplot()  
    geom_point(data = points, 
       aes(x = x, 
           y = y, 
           color = AgeGroup),
       size = 0.5)   
  labs(x = element_blank(),
       y = element_blank())  
  theme_bw()

g1

CodePudding user response：

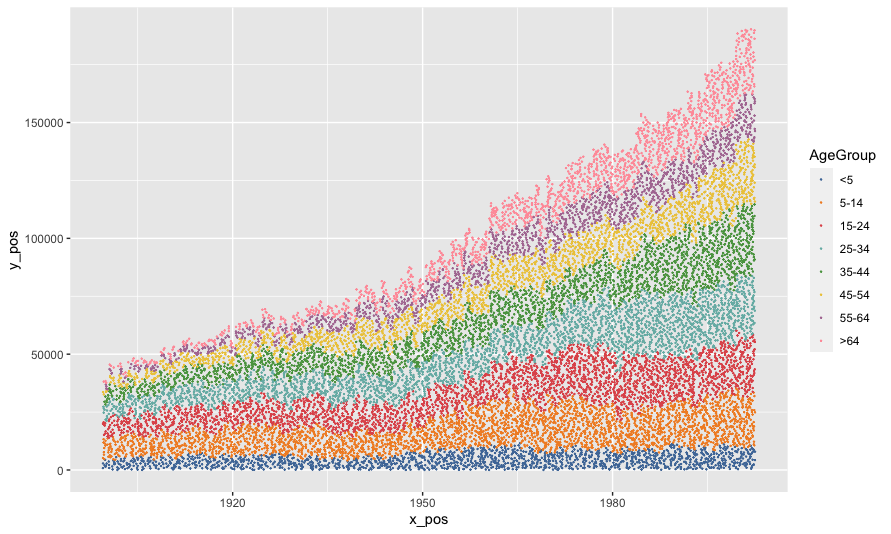
Here's a version without any smoothing, just adding noise to where the dots would go naturally. One nice thing here is we can specify how many people are represented per dot.

dots_per_thou <- 1
uspopage %>%
  uncount(round(dots_per_thou * Thousands / 1000)) %>%
  group_by(Year) %>%
  mutate(x_noise = runif(n(), 0, 1) - 0.5,
         x_pos = Year   x_noise,
         y_noise = runif(n(), 0, 1000*dots_per_thou),
         y_pos = cumsum(row_number()   y_noise)) %>%
  ungroup() %>%

  ggplot(aes(x_pos, y_pos, color = AgeGroup))  
  geom_point(size = 0.1)  
  ggthemes::scale_color_tableau()

CodePudding user response：

You could come close-ish to that look with the ggbeeswarm package. It includes a few positions which "offset points within a category based on their density using quasirandom noise" (