How to make a program in Mathematica that is able to recognize this image and return the radius of the circular part of it?

CodePudding user response：

While curve extraction is possible the radius can be obtained quite simply, i.e.

img = Import["https://i.stack.imgur.com/LENuK.jpg"];
{wd, ht} = ImageDimensions[img];
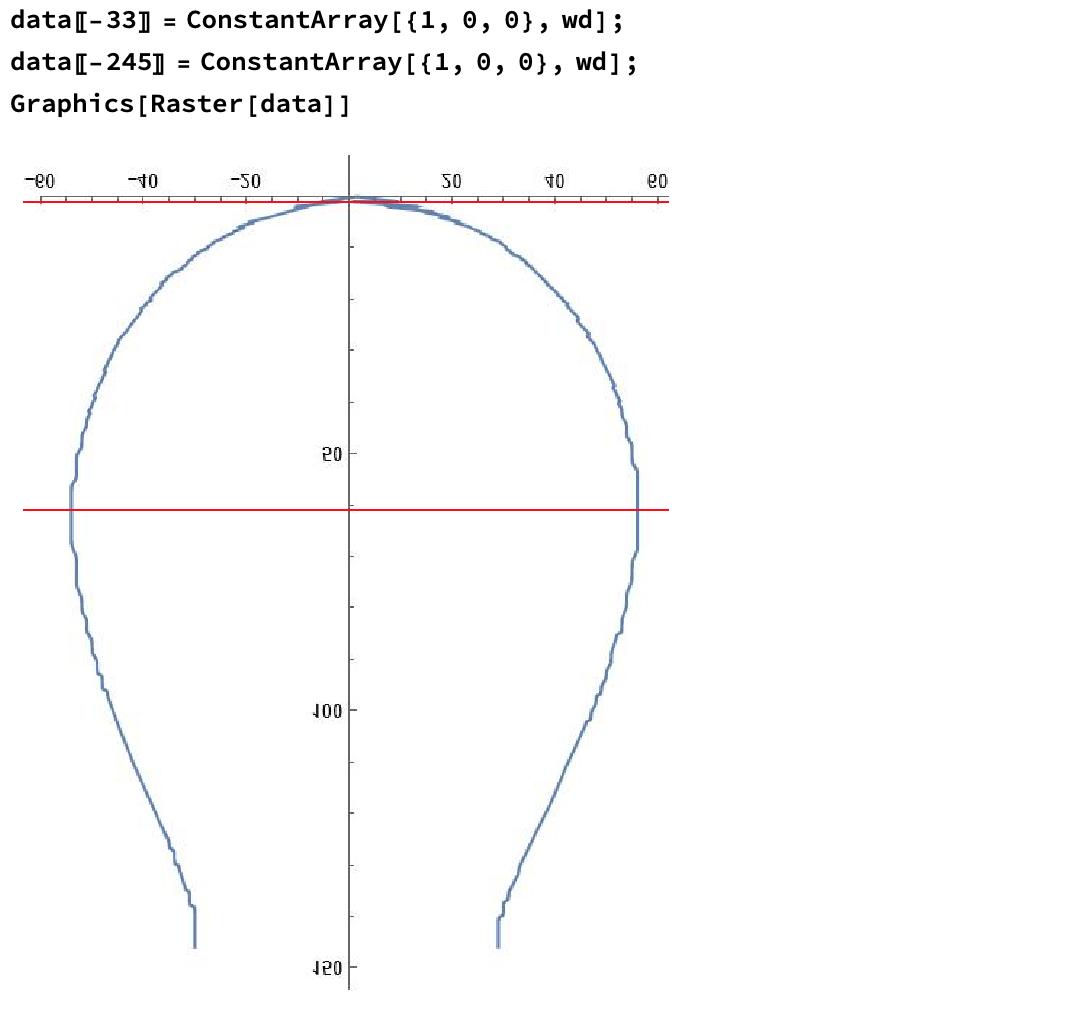
data = ImageData[img];
p1 = LengthWhile[data[[-33]], # == {1., 1., 1.} &];
p2 = LengthWhile[Reverse[data[[-33]]], # == {1., 1., 1.} &];
p120 = wd - p1 - p2 - 1;
p3 = LengthWhile[data[[-245]], # == {1., 1., 1.} &];
p4 = LengthWhile[Reverse[data[[-245]]], # == {1., 1., 1.} &];
pdrop = wd - p3 - p4 - 1;
radius = 120/p120*pdrop/2.

55.814

Further automation could automatically detect the widest point of the drop, which is here found by testing: line 245 (see sample lines in bottom image).

Making sense of the scale could be difficult to automate. We can see the outermost ticks are at -60 & 60, a length of 120 which turns out to be 400 pixels, pdrop.

As the sketch below shows, the circular part of the drop is limited by the widest points, so that length and the scale are all that is needed to find the radius.

Two lines are used to find the image scale and outer bounds of the drop: line 33 and 245, shown below coloured red.